|
Question 1104052: Hi! I got stuck with this problem...how should I go about solving this? 2(is less than or equal to) 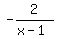 Thank you! Thank you!
Found 3 solutions by Alan3354, greenestamps, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The other tutor's solution is wrong....
The given inequality is

The other tutor simply multiplied both sides of the inequality by (x-1). That won't give you the full solution set; and it might give you a solution set which is NOT right. The problem with that method is that (x-1) might be negative; if it is, the direction of the inequality changes.
You can solve the problem by multiplying both sides of the inequality by (x-1); but you need to look at two cases -- when (x-1) is positive and when it is negative.
Case 1: If (x-1) is positive (that is, x>1), then




That is the "solution" that the other tutor gave; but it is not a solution at all. For this case 1, we are only considering solutions with x>1; "x <= 0" does not give any solutions with x>1.
So this first case gives us NO solutions to the inequality.
Case 2: If (x-1) is negative (that is, x<1), then
 [we multiplied by a negative; the direction of the inequality changes] [we multiplied by a negative; the direction of the inequality changes]



Since case 2 only considers values of x less than 1, the solution set for this case is 0 <= x < 1.
So the complete solution set is 0 <= x < 1; or, in interval notation, [0,1).
As an alternative to the above method of solution where we consider two different cases, we can modify the given inequality so that one side of the inequality is 0. Following is a solution to the problem using that strategy.





For x values less than 0, both numerator and denominator are negative, making the fraction positive; so x<0 is NOT part of the solution set.
For x values between 0 and 1, the numerator is positive and the denominator is negative, making the fraction negative; so x between 0 and 1 IS part of the solution set. Note the endpoint of that interval x=0 is part of the solution set, because it makes the numerator 0; the endpoint x=1 is NOT part of the solution set, because it makes the denominator 0.
For x values greater than 1, both numerator and denominator are positive, making the fraction positive; so x>1 is NOT part of the solution set.
And so the solution set -- as before, of course -- is [0,1)
Answer by ikleyn(52765)   (Show Source): (Show Source):
|
|
|
| |