SOLUTION: For an arithmetic sequence a₁₃ = 241 and common difference = 7. Determine the explicit formula and the first five terms of the sequence

Substitute n = 13, d = 7







Substitute a13 = 241



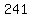
Subtract 84 from both sides



Back to



Substitute a1 = 157, d = 7







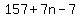
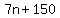 <--explicit formula

To find first five terms, write first term 157, and
add 7 successively to it and each preceding term to get the
next term:

157, 164, 171, 178, 185  <--first five terms

Edwin