Question 1103964: find four natural number in AP. such that their sum is 24 and their product is 945.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Different students would solve it different ways.
Different teachers would expect (maybe even require) different solutions.
Figure out what your teachers expects,
how you would solve the problem,
and how convenient it would be to please the teacher.
Some of the many possibilities are listed below.
THE FIFTH-GRADER WAY:
They must be easy small numbers to have a sum of  . .
As the product, 945, is odd,
all four numbers must be odd
 , ,
 , ,
 , ,
and any other sum of four odd numbers would be larger than  . .
So, is  equal to equal to  ? ?
It is obviously a multiple of  , of , of  and of and of  , ,
and  is also a multiple of is also a multiple of  . .
The four numbers must be  , ,  , ,  and and  . .
Let me check the product.

It checks, so the answer is  , ,  , ,  , and , and  . .
MY WAY (I like primes and prime factors):
Dividing by prime numbers in order,
we can find the prime factorization of  to be to be
 . .
Four numbers in arithmetic progression (arithmetic sequence in the USA)
with an average of  will have will have  as their mean and median, as their mean and median,
meaning that two of the four numbers will be less than 6,
and two will be more than 6.
The only integer factors that can be less than 6 are  and and  , ,
so re-writing  as a product of 4 integers, as a product of 4 integers,
 , ,
tells us the four natural numbers are
 , ,  , ,  , and , and  . .
THE ALGEBRA-AS-USUAL WAY:
An AP could be 6, 6, 6, 6, ....,
but in this case the product of four consecutive terms would be  , ,
so the numbers are not all the same;
one of them is less than the others.
Let  be the least of the natural numbers, and be the least of the natural numbers, and
 be the positive common difference be the positive common difference
(the difference between the least and the closest of the other 3 numbers).
That makes the numbers
 , , 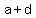 , , 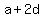 , and , and 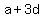 . .
The sum of the four numbers is
 . .
The sum of the four numbers is
 <--> <--> 
The product of the four numbers is
 --> -->  . .
So the answer is a solution of
 , ,
with  and and  being integers, being integers,
and  , so that it will be a natural number. , so that it will be a natural number.
THE ALGEBRA-WITH-COMMON-SENSE WAY:
As above, we get to
 , ,
and common sense tells us that
 and and  must be really common small numbers. must be really common small numbers.
In more mathematically rigorous words,
as 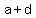 and and  are both natural numbers, with are both natural numbers, with 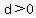 , ,
 is a positive integer (a natural number). is a positive integer (a natural number).
As  is a natural number, is a natural number,
 is an even natural number. is an even natural number.
Being the difference of two even numbers,
 must be an even number, must be an even number,
and as  is odd, is odd,  must be even. must be even.
Even numbers are 2, 4, 6, ...
 makes makes  , ,  , and , and  . .
The only solution is  , ,
which makes  , and , and  . .
So, the four natural numbers are
 , ,  , ,  , and , and  . .
THE ALGEBRA-WITH-A-TWIST (BUT NO COMMON-SENSE) WAY:
In an AP, the mean (average) is also the median,
so  is the median. is the median.
Let  be the common difference. be the common difference.
The four numbers are
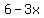 , ,  , , 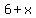 , and , and 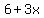 . .
Their product is






 --> -->  . .
 would give us negative numbers (not natural numbers) for the AP. would give us negative numbers (not natural numbers) for the AP.
 gives us gives us
 , ,  , ,  , and , and  . .
So, the four natural numbers are
 , ,  , ,  , and , and  . .
|
|
|