Question 1103833: A chemist has three different acid solutions. The first acid solution contains 15% acid, the second contains 30% acid, and the third contains 75% acid. He wants to use all three solutions to obtain a mixture of 216 liter containing 25% acid, using 2 times as much of the 75% solution as the 30% solution. How many liters of each solution should be used?
Found 2 solutions by ikleyn, josgarithmetic:
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website! .
Let x = the volume of the 15% acid (in liters) and
let y = the volume of the 30% acid.
Then the volume of the 75% acid is 2y liters.
Then your equations are
x + y + 2y = 216, (1) (total volume)
0.15x + 0.3y + 0.75*(2y) = 0.25*216 (2) (pure acid volume)
Simplify:
x + 3y = 216, (3)
0.15x + 1.8y = 54. (4)
Simplify one more time by multiplying eq(4) by 100 (both sides)
x + 3y = 216, (5)
15x + 180y = 5400. (6)
Now multiply eq(5) by 15 (both sides). The modified system is
15x + 45y = 3240, (7)
15x + 180y = 5400. (8)
Next subtract eq(7) from eq(8). The terms "15x" will cancel each other,
and you will get a single equation for only one unknown "y". (It is how the Elimination method works).
180y - 45y = 5400 - 3240,
135y = 2160 ====> y = 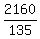 = 16.
Answer. 16 liters of the 30% solution, 16*2 = 32 of the 75% solution and the rest 216-(16+32) = 168 liters of the 15% solution.
Check. 0.3*16 + 0.75*32 + 0.15*168 = 54 liters of pure acid;
0.25*216 = 54 liters of pure acid. ! Correct !
Solved.
-----------------
There is entire bunch of introductory lessons covering various types of mixture problems
- Mixture problems
- More Mixture problems
- Solving typical word problems on mixtures for solutions
- Word problems on mixtures for antifreeze solutions
- Word problems on mixtures for alloys
- Typical word problems on mixtures from the archive
- Advanced mixture problems
- Advanced mixture problem for three alloys
in this site.
You will find there ALL TYPICAL mixture problems with different methods of solutions,
explained at different levels of detalization, from very detailed to very short.
Read them and become an expert in solution mixture word problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook in the section "Word problems" under the topic "Mixture problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by josgarithmetic(39617)  (Show Source):
|
|
|
