>>>A man can do a certain task in 21 hours,
So the man's rate in jobs per hour is
1 job per 21 hours or
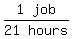 ,
so his rate in jobs/hour is
,
so his rate in jobs/hour is

>>>another man can do the task in 28 hours,
So the other man's rate in jobs per hour is
1 job per 28 hours or
 ,
so his rate in jobs/hour is
,
so his rate in jobs/hour is

>>>a boy can do the task in 48 hours
That's 1 job per 48 hours or
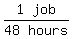 ,
so his rate in jobs/hour is
,
so his rate in jobs/hour is

>>>Find how long it will take to do the task if all three work.
Let x = the number of hours it will take all three to do the task.
Then their combined rate is
1 job per x hours or
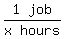 ,
so their combined rate in jobs/hour is
,
so their combined rate in jobs/hour is
 Their combined rate is also equal to the sum of their rates, so
Their combined rate =
Their combined rate is also equal to the sum of their rates, so
Their combined rate = 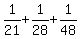

 So we set them equal:
So we set them equal:
 Cross-multiply
Cross-multiply


 hours
Edwin
hours
Edwin