SOLUTION: Find the perimeter of a right triangle whose hypotenuse is 2 and whose area is 2. Express your answer in simplest radical form.

Algebra ->  Finance -> SOLUTION: Find the perimeter of a right triangle whose hypotenuse is 2 and whose area is 2. Express your answer in simplest radical form.       Log On


   

Question 1103134: Find the perimeter of a right triangle whose hypotenuse is 2 and whose area is 2. Express your answer in simplest radical form.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39614) About Me  (Show Source):
Answer by ikleyn(52756) About Me  (Show Source):
You can put this solution on YOUR website!
.
The condition describes an IMPOSSIBLE situation,

and below I give the proof to this fact. 

Let the legs be x and y.


Then from the condition you have THESE two equations:

x^2 + y^2 = 2^2

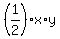%281%2F2%29%2Ax%2Ay = 2,


or, EQUIVALENTLY,

x^2 + y^2 = 4,   (1)
xy = 4.          (2)


Then  (x-y)^2 = x^2 -2xy + y^2 = (x^2+y^2) - 2xy = 4 - 2*4 = -4.


But the left side (x-y)^2 is a NON-NEGATIVE value/quantity,  while the right side is NEGATIVE.


Contradiction.

Conclusion: The condition is self-contradictory.