Question 1103106: Given that log(base a) x = p and log(base a) y = q, find the following: 1) log(base xy) a = ? and 2) log(base y) (ax^(2)y^(3)) = ?
I've been staring at this for a good twenty minutes and I cannot for the life of me figure it out. Any help is much appreciated. Thanks!
Found 2 solutions by KMST, ikleyn:
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The hardest to understand (and remember) properties of logarithms are
flipping base and number: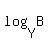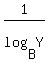   
and
change of base:   .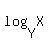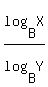
If you are going to "apply properties of logarithms" you need those two here.
You also need to know that  and that
 .
1) If you do not want to (or cannot) memorize or remember properties, you do not need to.
It all flows logically from the meaning of logarithm.
 means that  , and
 means that  .
That means that  ,
and if  .
Then, you understand that
    ,
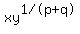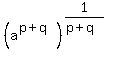and the fact that  means that
  .
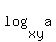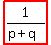INVOKING PROPERTIES OF LOGARITHMS:
1)
  .
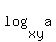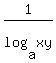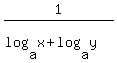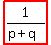2)
          
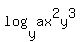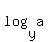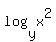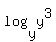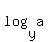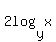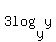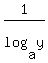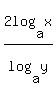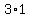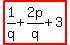
1) If you cannot memorize or remember properties, you do not need to.
It all flows logically from the meaning of logarithm.
means that , and
means that .
That means that ,
and if .
Then, you understand that
,
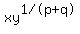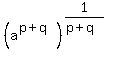and the fact that means that
.
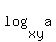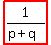NOTE:
The "properties of logarithms" sound like something to memorize,
and something to be anxious about,
but there is no need to be scared.
is read as
the logarithm on base of  is  .
The exponent on base to get is sounds easier,
by just replacing the word "exponent" for the scary word "logarithm."
Answer by ikleyn(52794)  (Show Source):
|
|
|
