Question 1103077: A positive integer is 11 less than another. If the sum of the reciprocal of the smaller and twice the reciprocal of the larger is 7/6, then find the two integers.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE FIFTH-GRADER APPROACH:
Let us try positive integers,
starting with  and and  , ,
and see if we bump into the solution.
The reciprocal are  and and  , ,
so the sum is
 , ,
and that works, so if there is just one solution,
as the question suggests,
the numbers are  and and  . .
THE ALGEBRA STUDENT APPROACH:
 = the smaller positive integer = the smaller positive integer
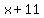 = the larger positive integer = the larger positive integer
 = the reciprocal of the smaller integer = the reciprocal of the smaller integer
 = twice the reciprocal of the larger integer = twice the reciprocal of the larger integer
The sum is

From here, we could say that
we multiply both sides of the equal sign times 
to eliminate denominators,
and get







At that point, knowing that x is a positive integer,
you know that factoring is an option.
Looking at the numbers, you see that  is a solution, is a solution,
because  . .
The factoring gives you
 , ,
and the positive inter solution is  , with , with  . .
The other solution is  , which is not a positive integer. , which is not a positive integer.
You could instead think of finding a common denominator,
and calculating step by step:







Same result, just not as elegant.
|
|
|