Question 1102843: Let n and r be positive integers with n ≥ r. Prove that rCr + (r+1Cr)+...+( nCr) = (n+1Cr+1)
Answer by math_helper(2461)   (Show Source):
You can put this solution on YOUR website! Proof by induction (using C(n,r) notation):
n=0: C(0,0) = 1 = C(1,1)
Assume its true for n=k:
n=k: C(r,r)+C(r+1,r)+ … + C(k-1,r) + C(k,r) = C(k+1, r+1) (*)
—
Now we need to show that it follows that (*) leads to the equality holding for n=k+1:
n=k+1: C(r,r)+C(r+1,r)+ … + C(k-1,r) + C(k,r) + C(k+1,r)
Adding brackets around all but the last term from above:
[ C(r,r)+C(r+1,r)+ … + C(k-1,r) + C(k,r) ] + C(k+1,r)
The part between brackets [ ] is (*):
= C(k+1, r+1) + C(k+1, r)
= 
—
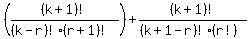
— re-writing the above by multiplying the 2nd term by (r+1)/(r+1) and
— pulling out the first factor of (k+1-r)! in the denominator:
—
= 
—
— allows us to factor to:
—
= 
—
= 
= 
= 
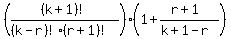
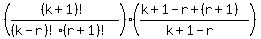
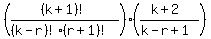
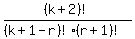
=  Done. Assuming truth for n=k ==> true for n=k+1
—
The last statement can be re-written as
= 
because n=k+1.
|
|
|
