Question 1102813: The equation r^2 = 4cos2θ is of the form r^2 = a^2 cos2θ, so the graph is a lemniscate. What is the length of each loop? At what values of θ do the endpoints of each loop occur? Sketch the graph of r^2 = 4cos2θ.
https://www.dropbox.com/s/0q9rpf0ywzip2tx/Screen%20Shot%202017-11-21%20at%209.17.53%20AM.png?dl=0
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! it must be  , so  <-->  .
That means that the 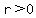 part of the curve stays within
a  angle from the horizontal x-axis.
As  ,  ,
and only for  is
 and  .
The endpoints of each loop occur for , with  .
For all other possible values of  ,
 , so  , and  .
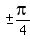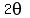As approaches  ,
 approaches  ,
and  approaches  .
The curve looks like an  symbol centered at the origin,
tangent to the slanted lines  .
For a better sketch, tabulate some ,  ,  , and  values, like
 .
|
|
|
