Question 1102804: An equation is given. (Enter your answers as a comma-separated list. Let k be any integer. Round terms to three decimal places where appropriate. If there is no solution, enter NO SOLUTION.)
2 cos(2θ) + 1 = 0
Find all solutions within the interval (0, 2pi).
Answer by ikleyn(52824)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
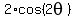 + 1 = 0 ====> + 1 = 0 ====>
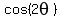 = =  ====> ====>
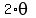 may have one of the two values: may have one of the two values: 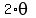 = =  or or 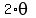 = =  .
Case 1. If .
Case 1. If 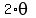 = =  , then the solutions for , then the solutions for  in the interval [0, in the interval [0, ) are these TWO values: ) are these TWO values:
 = =  and/or and/or  = = 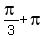 = =  .
Case 2. If .
Case 2. If 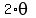 = =  , then the solutions for , then the solutions for  in the interval [0, in the interval [0, ) are these TWO values: ) are these TWO values:
 = =  and/or and/or  = = 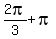 = =  .
Answer. The given equation has 4 (four, FOUR) solutions in the interval [0, .
Answer. The given equation has 4 (four, FOUR) solutions in the interval [0, ): ):
 , ,  , ,  , and , and  . .
The plot below visually confirms existing of 4 solutions:
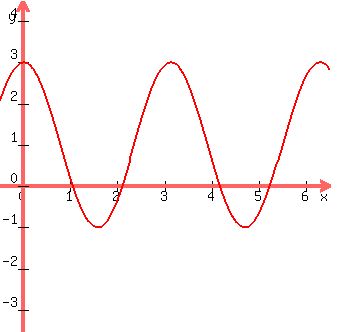
Plot y = 
SOLVED.
----------------
N O T E. All the part of the condition IN PARENTHESES makes no sense and IS NOT RELEVANT to the problem at all.
When I see such a NONSENSE in the condition, I become sad,
because I clearly see that the person who prepared this post does not understand WHAT HE IS WRITING.
|
|
|