SOLUTION: The average age of boys in a class of 30 is 15 years. If 10 more boys join the class, the average of the whole class gets reduced by a year. What is the average age of newcomers?

Algebra ->  Customizable Word Problem Solvers  -> Age -> SOLUTION: The average age of boys in a class of 30 is 15 years. If 10 more boys join the class, the average of the whole class gets reduced by a year. What is the average age of newcomers?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1102691: The average age of boys in a class of 30 is 15 years. If 10 more boys join the class, the average of the whole class gets reduced by a year. What is the average age of newcomers?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52794) About Me  (Show Source):
You can put this solution on YOUR website!
.
Since "The average age of boys in a class of 30 is 15 years", the sum of their ages is 30*15 = 450 years.


Let N be the average age of 10 newcomers.  Then the sum of their ages is 10N.


The total sum of 30 + 10 boys is 450 + 10N, and their average age is %28450%2B10N%29%2F%2830%2B10%29.


So, from the condition you have this equation


%28450%2B10N%29%2F40 = (15-1) = 14.


Then  450 + 10N = 14*40 = 560  ====>  10N = 560 - 450 = 110  ====>  N = 110%2F10 = 11.


Answer.  The average age of newcomers is 11 years.


Check.   %2830%2A15+%2B+11%2A10%29%2F40 = 14.   ! Correct !

Solved.


Or even simpler logical analysis: 

    Since "The average age of boys in a class of 30 is 15 years", the sum of their ages is 30*15 = 450 years.


    After joining 10 newcomers, the average age became 15-1 = 14 years;  hence, the sum of ages of all 40 students 
    of the class is 40*14 = 560 years now.


    The difference 560-450 = 110 years IS THE SUM of ages of the 10 newcomers.


    Hence, their average age is 110%2F10 = 11 years.

You got the same answer.

Surely, this "logical analysis" is the same solution, simply presented in the wording form.



Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


... and here is another solution using logical analysis -- similar to, yet very different from -- tutor ikleyn's second solution.

This is a method I like to use when a problem is about averages of numbers that are all "close together".

The average of the 30 boys originally in the class is 15.

After the 10 new boys join the class, the average of all 40 boys is 14; the average age went down by 1 year.

On average, each of the 30 boys originally in the class is 1 year older than the new average; that means all together their ages are a total of 30 more than what is needed to make the new average.

The total of the ages of the 10 new boys has to balance out those 30 "extra" years from the original 30 boys; that means the average age of the 10 new boys has to be 30/10 = 3 years LESS than the new average.

Since the new average is 14, the average age of the 10 new boys is 14-3 = 11.

With practice, this solution method is easy to use. We can see how the method works by representing it symbolically, like this:

(1) Let A be the new average.
(2) The sum of the ages of the original 30 boys in the class is 30%28A%2B1%29+=+30A%2B30.
(3) The new average, with 40 boys, is A; you want the total of the ages of all 40 boys to be 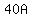40A.
(4) From (2) and (3), we see that the total of the ages of the 10 new boys has to be 40A+-+%2830A%2B30%29+=+10A-30.
(5) And that means the average age of the 10 new boys must be %2810A-30%29%2F10+=+A-3
And since the new average is 14, the average age of the 10 new boys is 14-3 = 11.