|
Question 1102598: I need help!! I need a rational function that crosses the x-axis at 3, touches the x-axis at -2, has vertical asymptotes at x=1 and x=-4, has a hole at x=5 and has a horizontal asymptote at y=2
I kind of figured out how to get it to do all except touching the x-axis at 2 and the hole at x=5. what am I doing wrong?
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Suppose a rational function is written with numerator consisting of a constant coefficient and linear factors of the form (x-a), and with the denominator consisting of linear factors of the form (x-a). Then...
(1) Each factor (x-a) that appears the same number of times in both numerator and denominator will produce a hole in the graph at x=a;
(2) Each factor (x-b) that appears only in the denominator will produce a vertical asymptote at x=b;
(3) Each factor (x-c) that appears only once (or any odd number of times) in the numerator will produce a root at x=c, with the graph crossing the x-axis at that point; and
(4) Each factor (x-d) that appears twice (or any even number of times) in the numerator will produce a root at x=d, with the graph just touching the x-axis at that point.
(5a) The graph of the rational function will have a horizontal asymptote of y=0 if the degree of the numerator is less than the degree of the denominator;
(5b) The graph will have a horizontal asymptote of y=k if the degrees of the numerator and denominator are equal and the constant coefficient is k.
Here is a rational function that shows most of these features, along with its graph (red) and the horizontal asymptote (green).
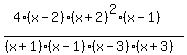

The constant coefficient 4, along with the fact that both numerator and denominator are of degree 4, produces the horizontal asymptote y=4 (item 5b above).
The identical factors of (x-1) in the numerator and denominator produce a hole in the graph at x=1 (item 1 above). The hole is not apparent in the graph produced by the software used on this site.
(If you graph this function on a good graphing calculator, with a small window either side of x=1, you should be able to see the hole.)
The factors (x+3), (x+1), and (x-3) in the denominator produce the vertical asymptotes at x=-3, x=-1, and x=3 (item 2 above).
The single factor (x-2) in the numerator produces a zero at x=2, with the graph crossing the x-axis at that point (item 3 above).
And the double factor of (x+2) in the numerator produces a double root at x=-2, with the graph just touching the x-axis at that point (item 4 above).
Use that example and the preceding discussion to determine the factors that are required for your example.
Notice that the requirements in your problem require...
(1) a single root (1 factor in the numerator);
(2) a double root (2 factors in the numerator);
(3) two vertical asymptotes (2 factors in the denominator); and
(4) a hole (1 factor each in numerator and denominator)
With only factors causing those features, the numerator has 4 linear factors while the denominator has only 3. If those were the only factors, then there would be no horizontal asymptote, as required. To get the required horizontal asymptote y=2, you need another factor in the denominator (producing a third vertical asymptote) to make the degrees of the numerator and denominator the same; and you need a constant coefficient 2 in the numerator.
That is why my example is similar to yours but has three vertical asymptotes instead of two.
|
|
|
| |