Question 1102544: Sally is going to buy a total of 11 new items at Target. She is going to buy jeans, dresses, and
shoes. She is going to spend exactly $460 and has discovered that jeans are $25, dresses are $50,
and shoes are $40. She is also going to buy twice as many shoes as jeans. Find out how many
jeans, how many shoes, and how many dresses she will buy?
Answer by ikleyn(52835)   (Show Source):
You can put this solution on YOUR website! .
Sally is going to buy a total of 11 new items at Target. She is going to buy jeans, dresses, and
shoes. She is going to spend exactly $460 and has discovered that jeans are $25, dresses are $50,
and shoes are $40. She is also going to buy twice as many shoes as jeans. Find out how many
jeans, how many shoes, and how many dresses she will buy?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x = the unknown number of jeans, and
let y = the unknown number of dresses.
Then the unknown number of shoes is 2x, according to the condition.
Now we can write our equations, TWO equations in TWO unknowns:
x + 2x + y = 11, (1) (counting for items)
25x + 40*(2x) + 50y = 460. (2) (counting dollars of spending)
Simplify the system:
3x + y = 11, (3)
105x + 50y = 460. (4)
To solve the system, I will apply the substitution method.
For it, express y = 11-3x from (3) and substitute it into eq(4). You will get
105x + 50*(11-3x) = 460 ====>
105x + 550 - 150x = 460 ====> -45x = 460 - 550 = -90 ====> x = 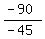 = 2.
Thus we found the unknown x. It is x= 2.
Then from eq(3) y = 11 - 3x = 11- 3*2 = 11-6 = 5.
Answer. 2 jeans, 2*2 = 4 shoes and 5 dresses.
Check. 2*25 + 4*40 + 5*50 = 460. ! Correct !
Solved.
----------------
The lesson to learn from this solution:
This problem is for 2 unknown.
It is not for 3 unknowns, as you may think at the first glance.
Solving with 2 unknowns is much easier than with 3 unknowns.
Therefore I made all the efforts required to solve it with 2 unknowns, not with 3.
|
|
|
