SOLUTION: log3 (x-4y+5)=0 and log3 (x-1)-log3 y=1 simaltenously

Learn how to change logarithm equations to and from 
equivalent exponential equations:

 and  are equivalent.

Therefore your first equation:

 is equivalent to

 and then



Your second equation:



Using a rule of logarithms, becomes

, which is equivalent to

 and then



Substituting 4y-4 for x:









Substituting in 











Since logs cannot be taken of negative numbers, and
the original second equation contains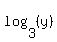  
and 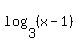, the only solutions are the
positive ones:

 and 

Edwin