Question 1102508: n the figure triangle abc is congruent to triangle bch which is congruent to triangle hgb is it possible to determine angle gbh why?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! When we say that triangle  is congruent to triangle  ,
we are saying about the relations of side length that.
 ,  , and  .
In this case, because side BC is shared between two triangles,
 .
So,  and 
That tells us that both triangles are at least isosceles,
and may even be a peculiar type of isosceles triangle
that we call an equilateral triangle.
I can also picture those two triangles looking like this
 , or like this  .
Without comparing sides of and  ,
we already know that they are both isosceles triangles,
with vertex marked by the middle letter and flanked by congruent sides:
 .
Angle HGB is the vertex angle of the isosceles triangle,
and angle GBH is one of the two congruent base angles.
We have three congruent isosceles triangles, looking like this
 ,
or like this  ,
or like this
 ,
or like this
 ,
but we do not know the measure of their angles.
It could be that they are equilateral,
with      ,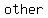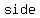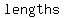
and all the angles measuring  .
However, without any more information
(which could be implied by the figure I do not see),
I do not know if they are equilateral triangles,
and I do not know the angles' measures.
|
|
|
