Question 1102223: What is the sum of all natural numbers between 1 and 200 which are multiples of 5?
Found 2 solutions by htmentor, greenestamps:
Answer by htmentor(1343)   (Show Source): (Show Source):
You can put this solution on YOUR website! The multiples of 5 between 1 and 200 are 5, 10, 15, ..., 200
This forms an arithmetic sequence with first term equal to 5 and common difference equal to 5.
The nth term is written a_n = 5 + (n-1)*5 = 5n
The sum of the 1st n terms of an arithmetic sequence is S_n = (n/2)(a + a_n),
where a = the 1st term
The last term is 200, so n = 200/5 = 40
S_40 = 20*(5 + 200) = 4100
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
This will be pretty much the same answer as provided by the other tutor, but using informal logical analysis instead of formal mathematical formulas.
Assuming that "between 1 and 200" includes 200, the sum is 5+10+...+195+200.
The number of terms in the sum is 200/5 = 40.
Since the numbers are equally spaced, the 40 numbers can be paired into 20 pairs, each with a sum of 205: 5+200 = 205; 10+195 = 205; 15+190 = 205; etc.
So the sum of all the numbers is the sum of 20 pairs, with each pair having a sum of 205: 205*20 = 4100.
And here is an alternative way to think about getting the final sum, once we have found that there are 40 terms in the sum.
Again since the numbers are equally spaced, the average of all the terms is the average of the first and last terms: (5+200)/2 = 102.5
Then the sum of all the numbers is that average, multiplied by the number of terms: 40(102.5) = 4100.
To summarize these two different ways of finding the sum, we have either
(a) (number of pairs)*(sum of first and last) = 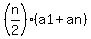
or
(b) (number of numbers)*(average of first and last) = 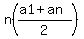
Those two formulas, representing different ways of thinking of getting the answer, are clearly mathematically equivalent.
|
|
|