SOLUTION: Becky is doing research in which she needs 28 grams of a substance that is 30% protein. How many grams of each two ingredients, one that is 50% protein and the other 25% protein, s

Algebra ->  Customizable Word Problem Solvers  -> Mixtures -> SOLUTION: Becky is doing research in which she needs 28 grams of a substance that is 30% protein. How many grams of each two ingredients, one that is 50% protein and the other 25% protein, s      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1102213: Becky is doing research in which she needs 28 grams of a substance that is 30% protein. How many grams of each two ingredients, one that is 50% protein and the other 25% protein, should she mix together?
Found 3 solutions by josgarithmetic, ikleyn, greenestamps:
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
system%28x%2By=28%2C25x%2B50y=30%2A28%29
-
5x%2B10y=6%2A28
5%2828-y%29%2B10y=6%2A28
5%2A28-5y%2B10y=6%2A28
5y=6%2A28-5%2A28
5y=28
y=28%2F5
highlight_green%28y=5%263%2F8%29-------grams of the 50% protein ingredient. Use this to find x.




--------------(THIS WAS WRONG)----------------------------------------------

system%28x%2By=28%2C30x%2B50y=25%2A28%29

30x%2B50%2828-x%29=25%2A28----simplify, solve for x, and evaluate y. x is for the 30% protein, and y is for the 50% protein ingredients.

Answer by ikleyn(52810) About Me  (Show Source):
You can put this solution on YOUR website!
.
Becky is doing research in which she needs 28 grams of a substance that is 30% protein. How many grams of each two ingredients,
one that is 50% protein and the other 25% protein, should she mix together?
~~~~~~~~~~~~~~~~~~ 

Let  x  be the amount of the 50% protein ingredient (in grams), and 
     y  be the amount of the 25% protein ingredient.

Then your equations are 

   x +     y = 28,         (1)    (total mass balance)
0.5x + 0.25y = 0.3*28.     (2)    (protein mass balance)


To solve it, multiply eq(2) by 2 (both sides). The modified system is

x +    y = 28,             (3)
x + 0.5y = 2*0.3*28        (4)


Now subtract eq(4) from eq(3).  The terms "x" will cancel each other, and you will get a single equation for y:

y - 0.5y = 28 - 2*0.3*28,   or

0.5y = 28 - 2*0.3*28 = 11.2  ====>  y = 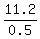11.2%2F0.5 = 22.4.


Answer.  22.4 grams of the 25% protein ingredient and (28-22.4) = 5.6 grams of the 50% protein ingredient is needed.


Check.   0.5*5.6 + 0.25*22.4 = 8.4.

         0.3*28              = 8.4.    ! Correct !


Be aware ! Writing by @josgarithmetic is INCORRECT !


Answer by greenestamps(13203) About Me  (Show Source):
You can put this solution on YOUR website!


The first tutor did indeed set up the problem incorrectly.
The second tutor gave a perfectly good solution by the standard algebraic process.

You can get the answer to mixture problems like this much faster and with much less effort using the method of alligation. (Do an internet search on "alligation" if you want to learn more about this method.)

Here is the diagram that is used to find the answer to your problem:

matrix%283%2C3%2C25%2C%22%22%2C20%2C%22%22%2C30%2C%22%22%2C50%2C%22%22%2C5%29

In the left column, the entries are the percentages of the two ingredients, 25 and 50.
In the middle column, the entry is the percentage of the mixture.
The numbers in the right column are found by finding the differences, diagonally, between the numbers in the first two columns: 50-30=20, and 30-25=5.

The numbers in the last column tell you the ratio in which the two ingredients must be mixed; the ratio of the 25% ingredient to the 50% ingredient needs to be 20:5, or 4:1.

So 4/5 of the total 28 grams must be the 25% ingredient, and 1/5 must be the 50% ingredient.

25% ingredient: %284%2F5%29%2A28+=+112%2F5+=+22.4 grams
50% ingredient: %281%2F5%29%2A28+=+28%2F5+=+5.6 grams

Once you understand how to use this method, it is MUCH faster than the traditional algebraic approach.