Question 1102109: Can someone explain me how to solve this. Thank you.
Find the values of x≥0 and y≥0 that maximize z=11x+15y, subject to each of the following sets of constraints.
(a) x+y≤19
x+2y≤24
b) x+5y≥10
5x+y≥15
x−y≤6
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13206)   (Show Source):
You can put this solution on YOUR website!
part a...
(1) Graph the inequalities to determine the feasibility region. Graph the boundary line for each inequality ( and  ); and find their point of intersection, which is (14,5).
Since both inequalities have "y <= ...", the feasibility region is the closed quadrilateral with vertices (0,0), (0,12), (14,5), and (19,0).
(2) Evaluate the objective function 11x+15y at each vertex to determine the maximum value.
(0,0): 11x+15y = 0
(0,12): 11x+15y = 180
(14,5): 11x+15y = 219
(19,0): 11x+15y = 209
The maximum value is 219, at (14,5).
Now here is an alternative for step (2) that will save you some time.
(a) Determine the slope of each constraint line and of the objective function:
x+y=19 --> y = -x+19 --> slope -1
x+2y=24 --> y = -(1/2)x+12 --> slope -1/2
11x+15y = ... --> y = (-11/15)x + ... --> slope -11/15
(b) Because the slope of the objective function is between the slopes of the two constraint lines, the maximum value of the objective function will be obtained at the intersection of the constraint lines.
(For further explanation of this method, if the slope of the objective function had been less than -1, the maximum value would have been obtained at (19,0); if the slope had been greater than -1/2, the maximum value would have been obtained at (0,12).
Using this method, you do not have to evaluate the objective function at every vertex of the feasibility region.
part (b)...
In this example, all of the constraint inequalities have "y >= ...", so the feasibility region is not closed. Therefore, it is not possible to maximize the objective function 11x+15y.
So I will assume in this case we are supposed to MINIMIZE the objective function.
When the three constraint boundary lines are graphed and the intersection points are determined, the coordinates of those intersection points are ugly fractions. So we will save a LOT of time and effort if we use the alternative method described above to determine where the minimum value of the objective function will be obtained.
x+5y=10 --> slope = -1/5
5x+y = 15 --> slope = -5
x-y=6 --> slope = 1
And the slope of the objective function is -11/15.
-11/15 is between -5 and -1/5; so the minimum value of the objective function will be obtained at the intersection of the boundary lines x+5y=10 and 5x+y=15.
Find the intersection point of those two lines and evaluate the objective function at that point.
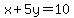
 [first equation, multiplied by 5]
 [difference of the previous two equations]
The intersection is (65/24,35/24).
The minimum value of the objective function is
Answer by ikleyn(52864)  (Show Source):
|
|
|
