Question 1102103: I have no idea how to calculate this. Appreciate the help. Thanks.
Solve the following linear programming problem.
Minimize: z=5x+30y
subject to: 9x+12y≥61
8x+4y≥32
x≥0, y≥0
What is the minimum value of z?
Found 2 solutions by stanbon, ikleyn:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! I have no idea how to calculate this. Appreciate the help. Thanks.
Solve the following linear programming problem.
Minimize: z=5x+30y
subject to:
9x+12y≥61
8x+4y≥32
x≥0, y≥0
What is the minimum value of z?
---------------
x >= 0 and y >= 0 means the answers are in the 1st quadrant
Solve the two other inequalities for "y"::
y >= (-3/4)x + (61/12)
y >= (-2)x + 8
--------------------
Plot those lines in Quadrant I
The y-intersects are (0,61/12) and (0,8)
The x-intersects are ([(61/12)/(3/4)],0) and (4,0)
---
Find the intersection of the two inequalities
(-3/4)x+(61/12) = -2x+8
(5/4)x = 3/4
x = 3/5
Then y = -2(3/5)+8 = 34/5
That vertex is (3/5,34/5)
-----
Find the 4 vertex polygon in Quadrant I including (0,0)
Vertices:: (0,0) ; (0,5) ; (4,0) ; (7/3,10/3)
-----
Check for z in z = 5x+30y for each of the (x,y) pairs
(0,0):: z = 5*0+30*0 = 0
(0,5):: z = 5*0+30*5 = 150
(4,0):: z = 5*4+30*0 = 20
(7/3,10/3):: z = 5(7/3)+30(10/3) = [35+300]/3 = 112 when rounded
-----
Ans:: Minimum z is zero
----------------------
Cheers,
Stan H.
---------------
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
First inequality 9x + 12y >= 61 is THIS restriction
y >= 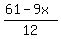 .
Second inequality 8x + 4y >= 32 is THIS restriction
y >= .
Second inequality 8x + 4y >= 32 is THIS restriction
y >= 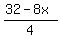 .
Together with the inequalities x >= 0, y >= 0 they form THIS feasibility domain in the first quadrant QI, shown in the Figure below: .
Together with the inequalities x >= 0, y >= 0 they form THIS feasibility domain in the first quadrant QI, shown in the Figure below:
 Plot y >=
Plot y >= 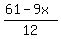 (over the read line) and y >= (over the read line) and y >= 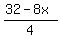 (over the green line)
Feasibility domain is INFINITE AREA in Q1 OVER the both red and green lines.
Feasibility domain has 3 vertices:
P1 = (0,8) (y-intercept to green line);
P2 = (7/3,10/3) (intersection point of the red and green line);
P3 = (61/9,0) (x-intercept to red line).
You should calculate the value of the objective function Z = 5x + 30y at these three points:
at P1: Z = 5*0 + 30*8 = 240;
at P2: Z = 5*(7/3) + 30*(10/3) = 111.667;
at P3: Z = 5*(61/9) + 30*0 = 33.889.
The minimum is achieved at the point P3 = (61/9,0), where x= 61/9, y=0, and is equal to 305/9 = 33.889 (approximately). (over the green line)
Feasibility domain is INFINITE AREA in Q1 OVER the both red and green lines.
Feasibility domain has 3 vertices:
P1 = (0,8) (y-intercept to green line);
P2 = (7/3,10/3) (intersection point of the red and green line);
P3 = (61/9,0) (x-intercept to red line).
You should calculate the value of the objective function Z = 5x + 30y at these three points:
at P1: Z = 5*0 + 30*8 = 240;
at P2: Z = 5*(7/3) + 30*(10/3) = 111.667;
at P3: Z = 5*(61/9) + 30*0 = 33.889.
The minimum is achieved at the point P3 = (61/9,0), where x= 61/9, y=0, and is equal to 305/9 = 33.889 (approximately).
To see other mini-max problems solved by the Linear Programming method, look into the lesson
- Solving minimax problems by the Linear Programming method
in this site.
|
|
|