Question 1102052: A class consists of 15 men and 17 women. Find the number of ways that the people in the class can arrange themselves in the following cases. (i) How many groups can be chosen from this class which consists of 7 men and 10 women?
Answer: C(15,7) * C(17,10) = 125147880
(ii)If two students have to be in the same group, how many groups of 12 students can be formed from this class?
Answer: 1 x C(30,10) + C(30,12) =
(iii) If one male A and one female B cannot be in the same committee, how many ways can a committee consisting of 4 men and 4 women be chosen from the class?
Answer: A committee consisting of 4 men and 4 women:
C(15,4) * C(17,4) = 3248700
From 3248700 subtract the cases where that male A and female B in the same committee. In those case we choose 3 men from the other 14 and 3 women from the other 16, so the number must subtract is:
C(14,3) * C(16,3) =364 * 560 = 203840 => 3248700 - 203840 = 3044860
Answer by ikleyn(52910)   (Show Source):
You can put this solution on YOUR website! .
A class consists of 15 men and 17 women. Find the number of ways that the people in the class can arrange themselves in the following cases.
(1) How many groups can be chosen from this class which consists of 7 men and 10 women?
Answer: C(15,7) * C(17,10) = 125147880 <<<---=== Correct !
(2) If two students have to be in the same group, how many groups of 12 students can be formed from this class?
Answer: 1 x C(30,10) + C(30,12) = <<<---=== This answer is NOT correct.
Notice that the gender of students IS NOT defined in this question.
So, you have these two students just ASSIGNED to each group,
and you can add only 10 additional arbitrary students from remaining 15+17-2 = 30 students.
So, the answer in this case is  .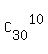
(3) If one male A and one female B cannot be in the same committee, how many ways can a committee consisting of 4 men and 4 women
be chosen from the class?
Answer: A committee consisting of 4 men and 4 women: C(15,4) * C(17,4) = 3248700
From 3248700 subtract the cases where that male A and female B in the same committee.
In those case we choose 3 men from the other 14 and 3 women from the other 16, so the number must subtract is:
C(14,3) * C(16,3) =364 * 560 = 203840 => 3248700 - 203840 = 3044860
I agree. It is correct.
Checked.
|
|
|
