.
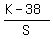 =
=  , (1)
, (1)
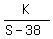 =
= 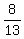 . (2)
================>
5*(K-38) = 2S, (3)
13K = 8*(S-38). (4)
================>
5K - 2S = 5*38, (5)
13K - 8S = -8*38. (6)
Multiply eq(5) by 4 (both sides). The modified system is
20K - 8S = 20*38, (7)
13K - 8S = -8*38. (8)
Now subtract eq(7) from eq(8) (both sides). You will get
20K - 13K = 20*38 - (-8)*38, or
7K = 20*38 + 8*38 = 28*38 ====> K =
. (2)
================>
5*(K-38) = 2S, (3)
13K = 8*(S-38). (4)
================>
5K - 2S = 5*38, (5)
13K - 8S = -8*38. (6)
Multiply eq(5) by 4 (both sides). The modified system is
20K - 8S = 20*38, (7)
13K - 8S = -8*38. (8)
Now subtract eq(7) from eq(8) (both sides). You will get
20K - 13K = 20*38 - (-8)*38, or
7K = 20*38 + 8*38 = 28*38 ====> K = 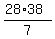 = 4*38 = 152.
Then from (5), 2S = 5K - 2*38 = 5*152 - 2*38 = 684 ====> S =
= 4*38 = 152.
Then from (5), 2S = 5K - 2*38 = 5*152 - 2*38 = 684 ====> S = 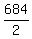 = 342.
Answer. K = 152, S = 342.
= 342.
Answer. K = 152, S = 342.