SOLUTION: What is the area of a rectangle whose perimeter is 92 and the diagonal of 34.

Algebra ->  Rectangles -> SOLUTION: What is the area of a rectangle whose perimeter is 92 and the diagonal of 34.      Log On


   

Question 1101805: What is the area of a rectangle whose perimeter is 92 and the diagonal of 34.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39630) About Me  (Show Source):
You can put this solution on YOUR website!
Rectangle's dimensions x and y

system%28x%2By=92%2F2%2Cx%5E2%2By%5E2=34%5E2%29

Solve the system and evaluate xy.

Answer by ikleyn(52879) About Me  (Show Source):
You can put this solution on YOUR website!
.
Let x and y be the dimensions of the rectangle.


2x + 2y = 92,   hence

 x + y = 46.               (1)


The second equation is

sqrt%28x%5E2+%2B+y%5E2%29 = 34,   or

x^2 + y^2 = 34^2           (2)


Square both sides of eq(1). You will get


x^2 + 2xy + y^2 = 46^2.    (3)


Now subtract eq(2) from eq(3) (both sides).  The terms  x^2  and  y^2 will cancel each other, and you will get


2xy = 46^2 - 34^2  =  (46-34)*(46+34) = 12*80.


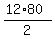Hence,  xy = %2812%2A80%29%2F2 = 6*80 = 480.


It is the area of the rectangle, which is under the question.


Answer.  The area of the rectangle is 480 square units.