The television show Pretty Betty has been successful for many years.
That show recently had a share of 31, meaning that among the TV sets
in use, 31% were tuned to Pretty Betty. Assume that an advertiser
wants to verify that 31% share value by conducting its own survey,
and a pilot survey begins with 14 households have TV sets in use at
the time of a Pretty Betty broadcast.
You can do these either by reasoning, formula or by calculator.
Find the probability that none of the households are tuned to Pretty Betty.
P(none) = ?
By reasoning.
The probability that the 1st person in the server didn't watch
it is 69% or 0.69.
The probability that the 2nd person in the server didn't watch
it is 69% or 0.69.
...
The probability that the 14th person in the server didn't watch
it is 69% or 0.69.
That's (0.69)×(0.69)×∙∙∙×(0.69) = (0.69)14 = 0.0055448177
By formula:
n=14 trials, probability p=0.31, x=0 successes
=
=
=
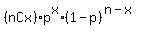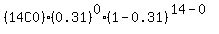= 0.005548177
Or by calculator:
binompdf(14,0.31,0) = 0.005548177.
Find the probability that at least one household is tuned to Pretty Betty.
P(at least one) = ?
That's the complement of the preceding problem, because if none
didn't, then at least one did.
1 - 0.005548177 = 0.9944551823
Find the probability that at most one household is tuned to Pretty Betty.
P(at most one) =
That's either none or one.
The first problem is the probability for none, 0.005548177.
So we need to add to that the probability that exactly 1 of the 14
watched it:
Then he probability that the 1st person in the survey watched it
and the other 13 did not, is (0.31)(0.69)13
Then he probability that the 2nd person in the survey watched it
and the other 13 did not, is (0.31)(0.69)13
...
Then he probability that the 14th person in the survey watched it
and the other 13 did not, is (0.31)(0.69)13
That's [(0.31)(0.69)13]×[(0.31)(0.69)13]×∙∙∙×[(0.31)(0.69)13] = (0.69)14 = 0.0348760996
So we add that to 0.005548177 and get
0.005548177 + 0.0348760996 = 0.0404209173
By formula:
n=14 trials, probability p=0.31, x=1 success
=
=
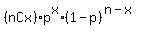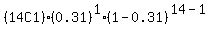= 0.0348760996
Total for 0 and 1 is 0.005548177 + 0.0348760996 = 0.0404209173
Or by calculator:
binomcdf(14,0.31,1) = 0.0404209173.
On the calculator notice that we used binomPdf for the first problem
because it was just one Particular value. But we used binomCdf for
the last problem because it was the Cumulative values of 0 and 1.
Edwin
