Question 1101554: Suppose a rational function has poles at x=1
x
=
1
and x=2
x
=
2
, zeros at x=4
x
=
4
and x=5
x
=
5
, and a horizontal asymptote y=3
y
=
3
. Find a possible rational function that has the attributes listed above.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
To have a pole at x=a, the denominator of the rational function must contain a factor of (x-a).
In your example, with poles at x=1 and x=2, we need factors of (x-1) and (x-2) in the denominator.
To get a zero at x=b, the numerator of the rational function must contain a factor of (x-b).
In your example, with zeros at x=4 and x=5, we need factors of (x-4) and (x-5) in the numerator.
To get a horizontal asymptote of y=3, we need the degrees of the numerator and denominator to be the same, and we need the leading coefficient in the numerator to be 3 times the leading coefficient in the denominator.
The simplest rational function that satisfies all these requirements is
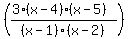
|
|
|