SOLUTION: Need help solving the oblique triangle. If angle C = 30° side a = 5 side b = 5 https://www.dropbox.com/s/c2hmsf45dnu7t18/Screen%20Shot%202017-11-12%20at%209.10.59%20AM.png?

Algebra ->  Trigonometry-basics -> SOLUTION: Need help solving the oblique triangle. If angle C = 30° side a = 5 side b = 5 https://www.dropbox.com/s/c2hmsf45dnu7t18/Screen%20Shot%202017-11-12%20at%209.10.59%20AM.png?      Log On


   

Question 1101510: Need help solving the oblique triangle.
If angle C = 30°
side a = 5
side b = 5
https://www.dropbox.com/s/c2hmsf45dnu7t18/Screen%20Shot%202017-11-12%20at%209.10.59%20AM.png?dl=0'
What is side c, angle A, and angle B ?
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
  

Since sides a and b are both equal, ΔABC is isosceles,
and ∠A = ∠B.  Suppose ∠A = ∠B = x,
then since ∠A+∠B+∠C = 180°,

x + x + 30° = 180°
   2x + 30° = 180°
         2x = 150°
          x = 75°

Therefore ∠A and ∠B are 75° each.

To find the length of side c, we draw the median CD (in green),
which since ΔABC is isosceles, is also the perpendicular
bisector of side c and the bisector of ∠C.

 

Therefore ΔBCD is a right Δ, and ∠BCD = 15°. 

We also know that BD is half of AB which is side c.

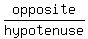
BD%2FBC%22%22=%22%22opposite%2Fhypotenuse%22%22=%22%22sin%28%2215%B0%22%29

BD%2F5%22%22=%22%22sin%28%2215%B0%22%29

We multiply both sides by 5

BD%22%22=%22%225sin%28%2215%B0%22%29

Using calculator:

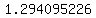BD%22%22=%22%221.294095226

Side c is twice that or

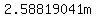c%22%22=%22%222.58819041m

You can round it however you were told.

Edwin