SOLUTION: Write the given expression in terms of x and y only. cos(sin^-1(x) - tan^-1(y))

Algebra ->  Trigonometry-basics -> SOLUTION: Write the given expression in terms of x and y only. cos(sin^-1(x) - tan^-1(y))      Log On


   

Question 1101502: Write the given expression in terms of x and y only.
cos(sin^-1(x) - tan^-1(y))
Answer by Edwin McCravy(20059) About Me  (Show Source):
You can put this solution on YOUR website!
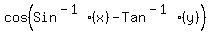
cos%28Sin%5E%28-1%29%28x%29+-+Tan%5E%28-1%29%28y%29%29
If we assume x and y are positive, then we can draw 
a couple of right triangles, one containing acute angle
A and one containing acute angle B.

A%22%22=%22%22 and B%22%22=%22%22

A is the angle whose sine is x, or x/1, so since the sine is the
opposite over the hypotenuse we put x on the opposite side of A
and 1 on the hypotenuse, then use the Pythagorean theorem to calculate
the adjacent side.

B is the angle whose tangent is y, or y/1, so since the tangent is the
opposite over the adjacent we put y on the opposite side of B
and 1 on the adjacent side, then use the Pythagorean theorem to calculate
the hypotenuse. 



So 

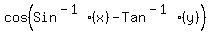
cos%28Sin%5E%28-1%29%28x%29+-+Tan%5E%28-1%29%28y%29%29%22%22=%22%22

cos%28A-B%29%22%22=%22%22cos%28A%29cos%28B%29%2Bsin%28A%29sin%28B%29%22%22=%22%22

%22%22=%22%22

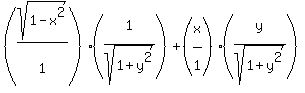
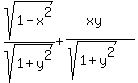
sqrt%281-x%5E2%29%2Fsqrt%281%2By%5E2%29%2B%28xy%5E%22%22%29%2F%28sqrt%281%2By%5E2%29%29%22%22=%22%22

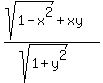%28sqrt%281-x%5E2%29%2Bxy%5E%22%22%29%2F%28sqrt%281%2By%5E2%29%29

Warning:  This solution assumes that x and y are both positive,
which puts the angles A and B both in quadrant I.  
If x and/or y were negative then A and/or B could be in other 
quadrants, which would cause one or both of the terms in the
numerator to have negative signs.

Edwin