|
Question 1101234: Given the equation 25x^2+y^2-100x+8y+91=0
a. Write the equation in the standard form
b. Find the coordinates of the center, foci, vertices, andd co-vertices
c. Sketch the graph of the ellipse
Answer by ikleyn(52772)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Given the equation 25x^2+y^2-100x+8y+91=0
a. Write the equation in the standard form
b. Find the coordinates of the center, foci, vertices, andd co-vertices
c. Sketch the graph of the ellipse
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Technically speaking, you need to complete squares separately for x- and y- terms.
25x^2 + y^2 - 100x + 8y + 91 = 0 is equivalent to
(25x^2 - 100x) + (y^2 + 8y) = - 91 is equivalent to
25*(x^2 - 4x) + (y^2 + 8y) = -91 is equivalent to
25*(x^2 - 4x + 4) + (y^2 + 8y + 16) = -91 + 100 + 16 is equivalent to
25*(x-2)^2 + (y+4)^2 = 25 (<<<---=== divide by 25 both sides ===--->>>) is equivalent to
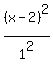 + +  = 1.
The last equation is the standard form equation of the ellipse
- centered at the point (2,-4)
- with the major axis parallel to y-axis
- taller than wide
- with the major semi-axis of the length of 5 in vertical direction and
the minor semi-axis of the length of 1 in horizontal direction.
The linear eccentricity of the ellipse is = 1.
The last equation is the standard form equation of the ellipse
- centered at the point (2,-4)
- with the major axis parallel to y-axis
- taller than wide
- with the major semi-axis of the length of 5 in vertical direction and
the minor semi-axis of the length of 1 in horizontal direction.
The linear eccentricity of the ellipse is 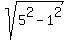 = =  = = 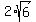 .
The vertices are (2,-4+5) = (2,1) and (2,-4-5) = (2,-9).
The co-vertices are (2+1,-4) = (3,-4) and (2-1,-4) = (1,-4).
The foci are (2,-4+ .
The vertices are (2,-4+5) = (2,1) and (2,-4-5) = (2,-9).
The co-vertices are (2+1,-4) = (3,-4) and (2-1,-4) = (1,-4).
The foci are (2,-4+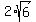 ) and (2,-4- ) and (2,-4-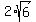 ).
The plot is THIS: ).
The plot is THIS:
 Ellipse
Ellipse 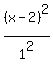 + +  = 1 = 1
See the lessons
- Ellipse definition, canonical equation, characteristic points and elements
- Standard equation of an ellipse
- Identify elements of an ellipse given by its standard equation
- Find the standard equation of an ellipse given by its elements
- General equation of an ellipse
- Transform a general equation of an ellipse to the standard form by completing the square
- Identify elements of an ellipse given by its general equation
Also, you have this free of charge online textbook in ALGEBRA-II in this site
ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic
"Conic sections: Ellipses. Definition, major elements and properties. Solved problems".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|
| |