SOLUTION: Find the dimensions of the rectangle with perimeter 20 units and area 24 square units.

(1)   2L + 2W = 20  ====>  L + W = 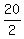 = 10

(2)   L*W = 24.


So, you need to find two numbers that sum up to 10 and multiply up to 24.


Answer.  The numbers are 6 and 4.    (3 seconds).

(1)  L + W = 10,    
(2)  L*W   = 24.


From (1), W = 10 - L.    Substitute it into eq(2). You will get

W*(10 - W) = 24.

10W - W^2 = 24  ====>  W^2 - 10W + 24 = 0  


     Next step you can apply the Vieta's theorem (if you know it) and to guess the roots mentally: 6 and 4.


     It is absolutely correct way. Moreover, if you will demonstrate such approach to your teacher, he (or she) will be happy.

     Or you can mentally factor the last equation to this equivalent form:  (W-6)*(W-4) = 0 and to get the roots in this way.

     But it is still based on the same guessing as in my solution #1 above, while I promised you "truly algebraic solution".


To keep my promise, I will apply the quadratic formula:

     =  = .


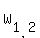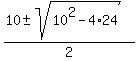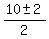Now the two solutions are 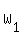  = 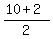 = 12/2 = 6  and  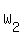 =  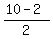= 8/2 = 4.


You got the same answer (happily !).


But now you are familiar with all basic methods of solutions, and you are ARMED with the knowledge !