Question 1101033: A stadium has 48,000 seats. Seats sell for $28 in section A, $16 section B, $12 section C. The numbers of seats in section A equals the total number of seats in section B and C. Suppose the stadium takes $1,016,800 from each sold-out event. How many seats does each section hold?
Answer by ikleyn(52782)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A stadium has 48,000 seats. Seats sell for $28 in section A, $16 section B, $12 section C.
The numbers of seats in section A equals the total number of seats in section B and C. Suppose the stadium takes $1,016,800
from each sold-out event. How many seats does each section hold?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x be the number of seats in section B, and y be the number of seats in section C.
Then the number of seats in section A is x+y, the sum of seats in sections B and C, according to the condition.
The condition says
seatsA + seatsB + seatsC = 48000, or
(x+y) + x + y = 48000, which is the same as
2(x+y) = 48000, which implies
x + y = 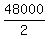 = 24000.
Thus we found that the sum of seats in sections B and C is 24000,
and, therefore, the number of seats in section A is 24000.
Thus we have now the problem FOR TWO UNKNOWNS only, since we just excluded A.
Now our system of two equations is
x + y = 24000, (1)
16x + 12y = 1016800 - 28*24000. (2)
Equation (2) express the money payed for seats in sections B and C together.
Simplify (1),(2) step by step:
x + y = 24000, (3)
16x + 12y = 344800. (4)
Multiply eq(1) by 16 (both sides). Then subtract eq(2) from it:
16x + 16y = 384000, (3)
16x + 12y = 344800. (4)
-------------------------
====> 4y = 384000-344800 = 39200 ====> y = = 24000.
Thus we found that the sum of seats in sections B and C is 24000,
and, therefore, the number of seats in section A is 24000.
Thus we have now the problem FOR TWO UNKNOWNS only, since we just excluded A.
Now our system of two equations is
x + y = 24000, (1)
16x + 12y = 1016800 - 28*24000. (2)
Equation (2) express the money payed for seats in sections B and C together.
Simplify (1),(2) step by step:
x + y = 24000, (3)
16x + 12y = 344800. (4)
Multiply eq(1) by 16 (both sides). Then subtract eq(2) from it:
16x + 16y = 384000, (3)
16x + 12y = 344800. (4)
-------------------------
====> 4y = 384000-344800 = 39200 ====> y = 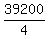 = 9800.
Then x = 24000 - y = 24000 - 9800 = 14200.
Answer. There are 24000 sears in section A, 14200 in section B and 9800 in section C. = 9800.
Then x = 24000 - y = 24000 - 9800 = 14200.
Answer. There are 24000 sears in section A, 14200 in section B and 9800 in section C.
|
|
|