You are studying about the question:
"When you alter the equation, how does that alter the graph?"
Here is the graph of  in red:
in red:
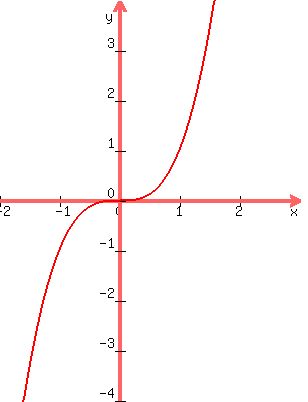 Next we take the right side of f(x), which is x3 and
replace x by x-1 and call it g(x). That graph has the exact same
shape as the graph of f(x) except that it is shifted 1 unit to the
right of f(x). Its graph is in green below, the graph of
Next we take the right side of f(x), which is x3 and
replace x by x-1 and call it g(x). That graph has the exact same
shape as the graph of f(x) except that it is shifted 1 unit to the
right of f(x). Its graph is in green below, the graph of

 Finally we take the right side of g(x), which is (x-1)3 and
add +2 and call it h(x). That graph has the exact same shape as the
graph of g(x), except that it is shifted (raised) 2 unit upward. Its
graph is in blue below, the graph of
Finally we take the right side of g(x), which is (x-1)3 and
add +2 and call it h(x). That graph has the exact same shape as the
graph of g(x), except that it is shifted (raised) 2 unit upward. Its
graph is in blue below, the graph of

 All three graphs have the same shape.
Edwin
All three graphs have the same shape.
Edwin