Question 1100978: The Smith family was one of the first to come to the U.S. They had 5 children. Assuming that the probability of a child being a girl is .5, find the probability that the Smith family had:
At least 2 girls :
At Most 2 girls :
Answer by greenestamps(13203)   (Show Source):
You can put this solution on YOUR website!
If the problem just asked for the probability of having EXACTLY 2 girls, then the calculation would be
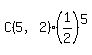 [choose 2 of the 5 children to be girls; the probability of either gender is 1/2 for each of the 5 children]
But in this problem, where you need to find the probability of at least two girls and then the probability of at most 2 girls, it is more efficient to use Pascal's Triangle, because all the entries in Pascal's Triangle are the C(n,r) "n choose r" numbers.
Note that we can use the numbers in Pascal's Triangle directly, because the probability of either gender is .5. For the same reason, you can use Pascal's Triangle directly if you are working problems involving flipping fair coins, where the probability of either heads or tails is .5.
For the probabilities with 5 children, you want to look at the 5th row of Pascal's Triangle, which is
1 5 10 10 5 1
Those numbers tell you that the probability of...
0 girls is 1/32
1 girl is 5/32
2 girls is 10/32 = 5/16
3 girls is 10/32 = 5/16
4 girls is 5/32
5 girls is 1/32
With all those numbers in front of you, it is easy to answer the questions.
P(at least 2 girls) = P(2 or 3 or 4 or 5) = 
And P(at most 2 girls) = P(0 or 1 or 2) = 
Of course you could also find the answer to the first question by calculating the probability of NOT having less than 2 girls:
P(at least 2 girls) = 1 - P(less than 2 girls) =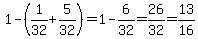 
|
|
|
