SOLUTION: Find the number of years it will take for $28,000 to grow to $29,718 at 6% interest compounded quarterly

Algebra ->  Finance -> SOLUTION: Find the number of years it will take for $28,000 to grow to $29,718 at 6% interest compounded quarterly       Log On


   

Question 1100973: Find the number of years it will take for $28,000 to grow to $29,718 at 6% interest compounded quarterly
Found 3 solutions by josgarithmetic, ikleyn, greenestamps:
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
Let n be number of compounding periods ( one fourth of a year each ).

28000%2A%281.015%29%5En=29718

-
log%28%2828000%29%29%2Bn%2Alog%28%281.015%29%29=log%28%2829718%29%29
n%2Alog%28%281.015%29%29=log%28%2829718%29%29-log%28%2828000%29%29
n%2A%280.006466%29=4.4730196-4.447158
n=%280.0258616%29%2F%280.006466%29
n=3.9996
closeenoughton=4----------four periods, same as 1 year

Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.
The formula is

FV = 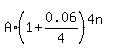A%2A%281+%2B+0.06%2F4%29%5E%284n%29


where FV is the Future Value, A is the original amount ($28,000), 0.06 = 6%,  4 (four) is the number of quarters in the year 
and n is the number of years.


The table is

n, year     FV

0	28000.00
1	29718.18
2	33477.31

Answer.   Exactly one year.

The solution,  the calculations and the answer by  @josgarithmetic   ("A little more than 9 years 11 months")  are   W R O N G.



Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!

The other tutor's answer is not right. Maybe you can see what her error was....

Her answer doesn't make sense. The $28000 at 6% interest for just one year without quarterly compounding would be $29680, so with compounding it will be close to the target value. So the answer should be something close to 1 year.

The annual interest rate is 6%, or .06; the quarterly interest rate is one-fourth of that, or .015. So we need to solve
28000%281.015%29%5En+=+29718
where n is the number of compounding periods (quarters of a year).

1.015%5En+=+29718%2F28000
n%2Alog%281.015%29+=+log%2829718%2F28000%29
n+=+log%2829718%2F28000%29%2Flog%281.015%29+=+4

So in fact the answer is that the $29718 value will be reached in 1 year with quarterly compounding.