Question 1100967: In a regular polygon each exterior angle is 150 degrees greater than each exterior. Calculate the number of sides
Found 2 solutions by KMST, ikleyn:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The question should state
"In a regular polygon each interior angle is 150 degrees greater than each exterior angle".
An exterior angle is the change of direction needed at each vertex to go around the polygon.
It is supplementary to the adjacent interior angle,
meaning that both of them add up to  . .
For example, here is a regular hexagon, with an interior angle and an exterior angle labeled as such:

In a regular polygon,
if each interior angle is 150 degrees greater than each exterior angle,
all exterior angles measure  degrees, degrees,
and all interior angles measure 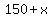 degrees, degrees,
 , ,  and and  . .
If you change direction by  degrees at each vertex, degrees at each vertex,
one whole turn going around the polygon, adding up a  turn, turn,
will require  changes of direction at changes of direction at  vertices, vertices,
and the polygon has  sides. sides.
The teacher wants you to remember that the sum of the interior angles of a polygon with  sides is sides is 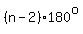 , ,
but without remembering,
you would intuitively know that for all polygons,
the sum of all exterior angles is  , ,
and it makes calculations faster/easier in this case.
Answer by ikleyn(52786)   (Show Source): (Show Source):
|
|
|