Question 1100944: The repair department of the bicycle shop repairs three things: flat tires, bent handle bars and
ripped seats. Today in the repair department, 25% of the bikes had flat tires only, 5% had bent
handlebars only, and 10% had ripped seats only. Just 1/12th of the bikes had all three repairs to
do: flat tires, bent handlebars and ripped seats. No bikes were completely fixed and there are a
total of 101 repairs to be made. How many bikes are in the repair department? How many bikes
need two repairs? If less than half of all the bikes have a ripped seat, what is the range of bikes
that need both the tires and handlebars repaired without needing to fix the seat?
Found 2 solutions by KMST, richwmiller:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! ONE APPROACH:
 = number of bikes in the shop waiting to be repaired. = number of bikes in the shop waiting to be repaired.
Of those,
25% have flat tires only,
5% have bent handlebars only, and
10% have ripped seats only.
That adds up to 25%+5%+10%=40% .
So, the number of bikes needing only 1 repair is
 . .
The number of bikes needing 3 repairs is  . .
The rest of the bikes is the fraction of all bikes that need exactly 2 repairs.
As a fraction of all the bikes, that is
 . .
As a number of bikes, it is
 . .
Counting the number of repairs needed, we have
 repairs for the repairs for the  bikes that need only 1 repair, bikes that need only 1 repair,
 repairs for the repairs for the 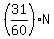 bikes that need exactly 2 repairs, bikes that need exactly 2 repairs,
and
 repairs for the repairs for the  bikes that need 3 repairs. bikes that need 3 repairs.
The number of repairs adds up to






There are  bikes in the repair department. bikes in the repair department.
Of those  bikes, bikes,
 need exactly two repairs, need exactly two repairs,
 , or , or  bikes, need all 3 repairs including their ripped seats, bikes, need all 3 repairs including their ripped seats,
25% , or  bikes, only need flat tires fixed, bikes, only need flat tires fixed,
5% , or  bikes, only need bent handlebars fixed, and bikes, only need bent handlebars fixed, and
10%, or  bikes only need their ripped seats fixed. bikes only need their ripped seats fixed.
In pictures, we could represent is as
 . .
The last question asks for the range of values for value of  , ,
The number of "bikes
that need both the tires and handlebars repaired without needing to fix the seat".
From the picture,
if  , ,  is the greatest possible is the greatest possible  ; ;
If  , ,  is the least possible is the least possible  . .
Without a picture:
If  is the total number of ripped seat repairs, is the total number of ripped seat repairs,
we do not know  exactly, but exactly, but
it includes at least the  that need only the seat repaired, that need only the seat repaired,
and the  that need all 3 repairs, so that need all 3 repairs, so
 or or  . .
If less than half the bikes have a ripped seat
(meaning  or less bikes), or less bikes),
we also know that  , so , so
 . .
If we exclude
those  bikes with ripped seats, bikes with ripped seats,
the  bikes that only need flat tires fixed, bikes that only need flat tires fixed,
and the  bikes that only need bent handlebars fixed, bikes that only need bent handlebars fixed,
we are excluding  , ,
what is left is the group of bikes that needs
"both the tires and handlebars repaired without needing to fix the seat."
That number is  . .
As  , ,

 . .
There are at least  and at most and at most 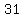 bikes that need bikes that need
"both the tires and handlebars repaired without needing to fix the seat."
The range can be expressed as [13,31], or as 
Answer by richwmiller(17219)   (Show Source): (Show Source):
|
|
|