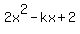

 The discriminant, which is b2-4ac, must be zero in
order for this equation to have just one real root:
The discriminant, which is b2-4ac, must be zero in
order for this equation to have just one real root:




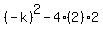

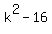 So we set this discriminant equal to zero:
So we set this discriminant equal to zero:
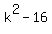

 Solve that either of two ways:
First way:
Solve that either of two ways:
First way:
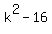

 Add 16 to both sides:
Add 16 to both sides:


 Use the principle of square roots:
Use the principle of square roots:


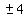 <-- the answers
Second way:
<-- the answers
Second way:
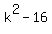

 Factor the left side as the difference of two squares:
Factor the left side as the difference of two squares:
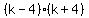

 k-4 = 0; k+4 = 0
k = 4; k = -4 <-- the answers
-------
To prove that
k-4 = 0; k+4 = 0
k = 4; k = -4 <-- the answers
-------
To prove that 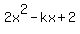

 just has one
real root when k = 4 or k = -4, we substitute in
just has one
real root when k = 4 or k = -4, we substitute in
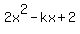

 Substituting 4 for k:
Substituting 4 for k:


 Divide both sides by 2
Divide both sides by 2


 Factor:
Factor:


 x-1 = 0; x-1 = 0
x = 1 x = 1 <-- just 1 root, 1
---
x-1 = 0; x-1 = 0
x = 1 x = 1 <-- just 1 root, 1
---
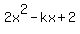

 Substituting -4 for k:
Substituting -4 for k:
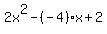


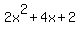

 Divide both sides by 2
Divide both sides by 2
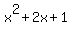

 Factor:
Factor:
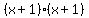

 x+1 = 0; x+1 = 0
x = -1 x = -1 <-- just 1 root, -1
Edwin
x+1 = 0; x+1 = 0
x = -1 x = -1 <-- just 1 root, -1
Edwin