Question 1100633: For x^4-6x^3+9x^2
A) use the coefficient test to determine the graph’s end behavior
B) Find the x-intercepts. State whether the graph crosses the x-axis, or touches the x-axis and turns around, at each intercept.
C) Find the y-intercept.
D) Determine whether the graph has y-axis symmetry, origin symmetry, or neither.
E) Find a few additional points and graph the function. Use the maximum number of turning points to check whether it is drawn correctly.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
For x^4-6x^3+9x^2
A) use the coefficient test to determine the graph’s end behavior
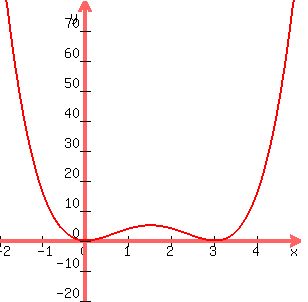
The degree of the polynomial is even, and the leading coefficient is positive, so the function value is going to positive infinity on both ends.
B) Find the x-intercepts. State whether the graph crosses the x-axis, or touches the x-axis and turns around, at each intercept.

There are two double roots, at x=0 and x=3. Since they are double roots, the graph just touches the x-axis at those points,
Note the answers to parts A and B tell us that the function value is never negative.
C) Find the y-intercept.
Set x equal to 0; the function value is 0. So the y-intercept is the origin.
(But we already knew that, because 0 is a root.)
D) Determine whether the graph has y-axis symmetry, origin symmetry, or neither.
It is a polynomial function with terms that are both even and odd powers, so it has neither y-axis symmetry nor origin symmetry.
E) Find a few additional points and graph the function. Use the maximum number of turning points to check whether it is drawn correctly.
I'm not sure what the instructions are asking you to do here....
Here is a graph:
|
|
|