|
Question 1100600: I have to make up an equation, using simultaneous equations, according to this question;
A father is 26 years older than his daughter. In 4 years, he will be 2 more than 5 times her age. Find out both their age.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52914)   (Show Source):
You can put this solution on YOUR website! .
A father is 26 years older than his daughter. In 4 years, he will be 2 more than 5 times her age. Find out both their age.
~~~~~~~~~~~~~~~~~~~~~~
Let x be the father's age, y be the daughter age.
The condition gives you these two equations
x - y = 26, (1) ("A father is 26 years older than his daughter")
x + 4 = 5*(y+4) + 2. (2) ("In 4 years, he will be 2 more than 5 times her age")
From eq(1), express x = 26+y and substitute it into eq(2). You will have
(26+y) + 4 = 5y + 20 + 2,
30 + y = 5y + 22 ====> 4y = 30-22 = 8 ====> y = 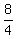 = 2.
Answer. The daugther is 2 years old, the father is 26 + 2 = 28 years old.
Check. In 4 years, father will be 28+4 = 32 years old.
The daughter will be 6 years old.
6*5 +2 = 32. ! Correct !
--------------
There is a bunch of lessons on age word problems
- Age problems and their solutions
- A fresh formulation of a traditional age problem
- Really intricate age word problem
- Selected age word problems from the archive
- Age problems for mental solution
in this site.
Read them and become an expert in solving age problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Age word problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13216)  (Show Source):
|
|
|
| |
