Question 1100490: What is the area of an equilateral triangle if a point inside the triangle is at a distance of 3, 4 and 5 cm from the vertices?
Found 3 solutions by Fombitz, ikleyn, greenestamps:
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! Use Viviani's theorem.
The height of the triangle is equal to the sum of the three lengths.

Now you know the height of the equilateral triangle, you can find the side length using the Pythagorean theorem and then the area.
Answer by ikleyn(52759)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The solution by the tutor @Fombitz relates to ANOTHER problem,
when the given distances are the distances to the SIDES of an equilateral triangle.
For that problem the solution is correct, BUT NOT FOR THE GIVEN problem.
Below I will try to analyze the problem. I got some equation for the unknown side length of the equilateral triangle.
But this equation is very complicated and does not allow analytical "exact" solution.
Nevertheless, it does allow to get some estimation for the solution, at least.
Before to start analyze, I made quick search in the Internet.
I didn't find the solution there. I found only some attempts to solve the problem, but these attempts did not go far.
It looks like that this problem is considered by those few people who tried solve it as unsolved and as not having direct,
simple, clear, elementary and straightforward solution.
Let x be the unknown side length under the question.
Let ABC be the given equilateral triangle, and let P be that point inside.
1. For the triangle APC with the sides 3 and 4 cm and the angle  = < APC we have from the cosine law = < APC we have from the cosine law
 = = 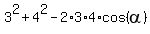 , or , or  = =  , so , so  = = 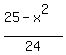 and then and then
 = =  = = 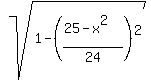 . (1)
2. For the triangle BPC with the sides 3 and 5 cm and the angle . (1)
2. For the triangle BPC with the sides 3 and 5 cm and the angle  = < BPC we have from the cosine law = < BPC we have from the cosine law
 = =  , or , or  = = 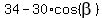 , so , so  = = 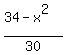 and then and then
 = =  = =  . (2)
3. For the triangle APB with the sides 4 and 5 cm and the angle . (2)
3. For the triangle APB with the sides 4 and 5 cm and the angle  = < APB we have from the cosine law = < APB we have from the cosine law
 = = 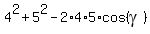 , or , or  = = 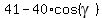 , so , so  = = 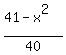 and then and then
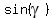 = = 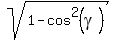 = = 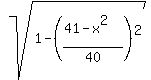 . (3)
4. Next, the area of the triangle APC is . (3)
4. Next, the area of the triangle APC is 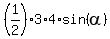 = =  . (4)
The area of the triangle BPC is . (4)
The area of the triangle BPC is  = = 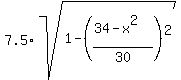 . (5)
The area of the triangle APB is . (5)
The area of the triangle APB is  = =  . (6)
5. Now I can make an equation by equating the area of the large triangle to the sum of the areas of small triangles . (6)
5. Now I can make an equation by equating the area of the large triangle to the sum of the areas of small triangles
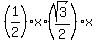 = =  + + 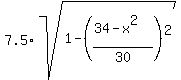 + +  , or, which is the same , or, which is the same
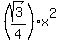 = =  + + 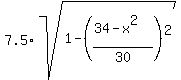 + +  .
6. It is the equation I talked about before to start my solution.
I will try to solve it graphically. .
6. It is the equation I talked about before to start my solution.
I will try to solve it graphically.
 Plot y =
Plot y = 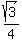 (red) and y = (red) and y =  + + 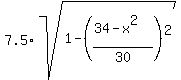 + +  (green)
I made also estimation for the root "x" using Excel in my computer and got x between 6.76 and 6.77: 6.76 < x < 6.77. (green)
I made also estimation for the root "x" using Excel in my computer and got x between 6.76 and 6.77: 6.76 < x < 6.77.
I invite and ask other tutors who has "a technology" in their hands to make their more precise estimations.
=========================
Great , @greenestamps ! ! !
Your solution is Excellent !
=========================
Answer by greenestamps(13196)   (Show Source): (Show Source):
You can put this solution on YOUR website!
This is the EXACT problem that, about 45 years ago, rekindled my interest in mathematical problem solving.
A college friend of mine who had become a junior high school math teacher sent it to me, and over the course of a couple of years I made various attempts at solving it. I know I finally came up with an answer after a huge amount of ugly mathematics; but that solution method is long lost.
It is lost because, when I looked at the problem for the umpteenth time, I found a quick and simple solution that gives an exact answer.
Here it is....
Call the equilateral triangle ABC, with interior point P. AP=3; BP=4, CP=5.
Make a copy of triangle BPC. Rotate that triangle 60 degrees about point B, so that the copy of side BC coincides with side BA. Make P' the "image" of point P.
Now consider quadrilateral BPAP'. Draw diagonal PP'.
Angle PBP' is 60 degrees; because it is still the sum of angles ABP and CBP.
But BP and BP' are both 4 units long; that makes triangle BPP' an equilateral triangle, so PP' is 4 units long, and angle BPP' is 60 degrees.
But now triangle APP' has side lengths 3, 4, and 5, so angle APP' is a right angle.
And that makes angle BPA 150 degrees.
And then the law of cosines gives us the exact length of the side s of triangle ABC; and from there we can find the area of triangle ABC.



The area of an equilateral triangle with side length s is  , so the area of the triangle is , so the area of the triangle is

It is always very gratifying to find a simple solution to a problem that for so long had seemed extremely difficult....
------------------------------------------------------------
Note tutor ikleyn's technology solution gives the right answer for the length of the side of the triangle:

which confirms her statement that the side length is between 6.76 and 6.77.
|
|
|