SOLUTION: if two mengo to a hospital in a room, before entring ,they have been asked to off their shoes and can enter .after returning ,the shoe keeper throw them the pairs randomly.find the

Algebra ->  Probability-and-statistics -> SOLUTION: if two mengo to a hospital in a room, before entring ,they have been asked to off their shoes and can enter .after returning ,the shoe keeper throw them the pairs randomly.find the      Log On


   

Question 1100390: if two mengo to a hospital in a room, before entring ,they have been asked to off their shoes and can enter .after returning ,the shoe keeper throw them the pairs randomly.find the probability that both have received their own pairs?
Answer by ikleyn(52898) About Me  (Show Source):
You can put this solution on YOUR website!
.
if two highlight%28cross%28mengo%29%29 men go to a hospital in a room, before highlight%28cross%28entring%29%29 entering,
they have been asked to off their shoes and can enter. After returning, the shoe keeper throw them the pairs randomly.
Find the probability that both have received their own pairs?
~~~~~~~~~~~~~~~~ 

If the shoe keeper throws them each pair as a whole thing (not as two separate pieces), 

then the probability under the question is  1%2F2.


-----------------------
Comment from student: Question 1100390: if two mengo to a hospital in a room, before entring , they have been asked
to off their shoes and can enter .after returning ,the shoe keeper throw them the pairs randomly.
find the probability that both have received their own pairs? And what if the number of men is not 2 but 20 in above question ?
Please solve the proper way to this problm kindly...nd send me
----------------------- 

My response: The full space of events is the space of all permutations of n items,

in this case, of 20 pairs of shoes.


Only ONE permutation is happy.


So, the probability under the question is 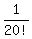 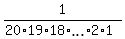1%2F20%21 = 1%2F+%2820%2A19%2A18%2Aellipsis%2A2%2A1%29.

Use your calculator to get the number . . .

Solved.


-----------------
On Permutations, see the lessons
    - Introduction to Permutations
    - PROOF of the formula on the number of Permutations
    - Problems on Permutations
in this site.

Also,  you have this free of charge online textbook in ALGEBRA-II in this site
    - ALGEBRA-II - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this online textbook under the topic  "Combinatorics: Combinations and permutations".


Save the link to this textbook together with its description

Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson

into your archive and use when it is needed.