Question 1100319: The car radiator holds 20L. It contains a 25% antifreeze solution. Since the weather is getting colder,
the mechanic should make the solution 40% antifreeze. How much of the 25% solution should be drained
and replaced with pure antifreeze to give a 40% solution.
Found 3 solutions by ikleyn, greenestamps, richwmiller:
Answer by ikleyn(52847)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The car radiator holds 20L. It contains a 25% antifreeze solution. Since the weather is getting colder,
the mechanic should make the solution 40% antifreeze. How much of the 25% solution should be drained
and replaced with pure antifreeze to give a 40% solution.
~~~~~~~~~~~~~~~~~~~~~
Let V be the volume to drain off from 20 liters of antifreeze.
Step 1: Draining. After draining, you have 20-V liters of the 25% antefreeze.
It contains 0.25*(20-V) of pure antifreeze.
Step 2: Replacing. Then you add V liters of the pure antifreeze (the replacing step).
After the replacing, you have the same total liquid volume of 20 liters.
It contains 0.25(20-V) + V liters of pure antifreeze.
So, your "concentration equation" is
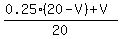 = 0.4. (1) <<<---=== It is the fraction of the pure antifreeze volume to the total volume.
The setup is done and completed.
To solve the equation (1), multiply both sides by 20. You will get
0.25*(20-V) + V= 0.4*20,
5 - 0.25V + V= 8,
0.75V = 8 - 5 = 3 ====> V = = 0.4. (1) <<<---=== It is the fraction of the pure antifreeze volume to the total volume.
The setup is done and completed.
To solve the equation (1), multiply both sides by 20. You will get
0.25*(20-V) + V= 0.4*20,
5 - 0.25V + V= 8,
0.75V = 8 - 5 = 3 ====> V =  = 4 liters.
Answer. 4 liters of the 25% antifreeze must be drained and replace by 4 liters of pure antifreeze.
Check. = 4 liters.
Answer. 4 liters of the 25% antifreeze must be drained and replace by 4 liters of pure antifreeze.
Check. 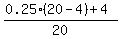 = 0.4. = 0.4.
-----------------
There is entire bunch of introductory lessons covering various types of mixture problems
- Mixture problems
- More Mixture problems
- Solving typical word problems on mixtures for solutions
- Word problems on mixtures for antifreeze solutions (*)
- Word problems on mixtures for alloys
- Typical word problems on mixtures from the archive
in this site.
Read them and become an expert in solution mixture word problems.
Notice that among these lessons there is one on antifreeze solutions marked by (*).
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook in the section "Word problems" under the topic "Mixture problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
=======================
Dear tutor @greenestamps !
I sincerely ask you to change RADICALLY your tone regarding my solutions.
What would be even better, if you stop to refer to my solutions at all,
except you see a direct error in it.
Thanks,
Ikleyn.
---------------------
And notice, please, that I keep very neutral tone regarding your solutions even when I see them not fully completed or even incorrect.
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor ikleyn is primarily a scientist, so she always starts these mixture problems with the "concentration equation" -- which is fine for someone who already knows how to solve this kind of problem and is familiar with that equation.
But I don't find that approach very useful for a student show is trying to LEARN HOW to solve this kind of problem.
So let me offer a different approach.
And the method I use is NOT the traditional algebraic approach taught in most beginning algebra classes.
Step 1: Analyze the problem and understand what is really significant. In this problem, it is irrelevant that some amount of the original 25% antifreeze solution is removed and replace with pure antifreeze. In the end, the problem simply involves mixing 25% antifreeze solution with pure antifreeze to get a 40% solution.
Step 2: Make a very rough estimate of what the answer should be. You will be mixing 25% antifreeze with 100% antifreeze to get a 40% antifreeze solution. Clearly you will need to use far more of the 25% solution than the pure 100% antifreeze.
Step 3: This is where my method is very different from the traditional method....
In step 2 we found by logical analysis that we need to use more of the 25% solution than the pure antifreeze to get a 40% solution. We can refine that analysis to solve the problem exactly. Specifically, the ratio in which the two ingredients must be mixed is exactly determined by where the 40% of the final mixture lies between the 25% and 100% of the two ingredients.
The 40% is 60% away from 100%; it is 15% away from the 25%.
Those differences of 60 and 15 mean that the two ingredients must be mixed in the ratio 60:15, or 4:1.
Since the radiator holds 20L, we must use 16L of one ingredient and 4L of the other.
And since we already logically concluded that we need more or the 25% than of the 100%, the answer is that we need 4L of the pure antifreeze and 16L of the original 25% antifreeze.
Then finally we need to go back and answer the exact question that was asked:
4L of the original antifreeze solution must be drained and replaced with pure antifreeze to get 20L of 40% antifreeze.
With all the words of explanation, this sounds like a long and tedious process. But without all the words, here is all that is involved in solving this problem:
100-40 = 60; 40-25 = 15
60:15 = 4:1
So 16L of the original and 4L of the pure antifreeze
Answer by richwmiller(17219)   (Show Source): (Show Source):
You can put this solution on YOUR website! Dear Ikleyn,
You are a smart person. Why are you getting upset?
Greenestamps was trying to explain why he offered another approach.
He did NOT say you were wrong. He was just offering a different approach.
You do the same thing as greenestamps.
You both offer added comments.
He offers a different approach than the normal algebraic solutions.
You offer solutions from your point of view.
As long as the original solution is correct, there really is no need for an additional solution.
Let's try to get along.
Rich
|
|
|