Question 1100248: Please help me solve this
Find the value of log(225/32)-log(25/81)+log(64/729)
Found 2 solutions by josgarithmetic, KMST:
Answer by josgarithmetic(39628)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! MAYBE THE SIMPLEST WAY IS
  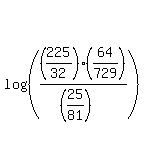    
As long as you properly key in
225 × 64 × 81 ÷ ( 32 × 729 × 25 ) or 225 × 64 × 81 ÷ 32 ÷ 729 ÷ 25 ,
your calculator will calculate the expression inside the log as
 , ,
so the answer is 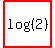 . .
Because I had been doing a lot of math before modern calculators,
I would calculate it with pen and paper as

ANOTHER WAY:
As a first step, you know that log of a quotient is the difference of the logs,
so

 
 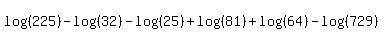 . .
Then you should realize that the only prime factors in all of those numbers are
 , ,  , and , and  . .
Math problems are rigged so that you can demonstrate understanding of concepts with easy arithmetic.
That works for school and for standardized tests.
Prime factorization helps here too; it's not only for adding fractions,
or factoring polynomials.
No need to stick to a factoring algorithm;
just to the factorization you think you need,
in whatever way works for you.

 . .
With the numbers written as products of factors, you apply that facts that
log of a product is the sum of the logs,
log of a power is the exponent times the log of the base.
So,  , ,
 , ,
and so on.
When you apply that you end up with a bunch of terms with
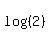 , , 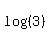 , and , and 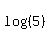 . .
You can "collect like terms" (adding apples with apples and oranges with oranges).
You should end up with at most three terms.
Then you can do the reverse work of making that sum of logs into a single log.
Putting it all together,

 
 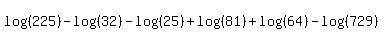
 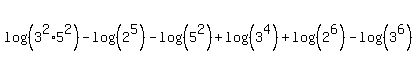
 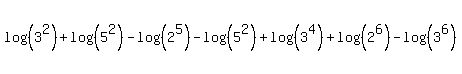
 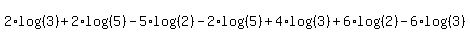
 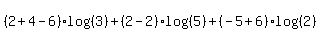
 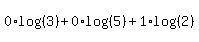
 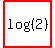
|
|
|