Question 1100247: When 64329 is divided by the number x, the successive remainders are 175,114 and 213. The sum of digit of x is?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There is a typo, or something was lost in translation here,
because the wording does not make sense.
SUGGESTED PROBLEM AND ITS SOLUTION:
If a number  was to be divided by was to be divided by  , ,
dividing successive quotients by 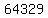 , ,
with  , , 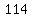 , and , and 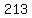 being the first successive remainders in that order, being the first successive remainders in that order,
calculating the sum the digits of  , ,
and repeating the adding of digits until a 1-digit sum was obtained,
the final sum of digits would be  . .
Why?
Adding digits of a number and the successive sums of digits,
the final sum is the remainder of dividing that number by  . .
The final sums for
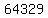 , , 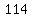 , and , and 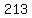
are multiples of  , ,
 , ,  and and 
meaning that 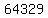 , , 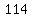 , and , and 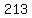 are multiples of are multiples of  . .
That would make the successive quotients multiples of  . .
With 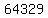 and the fist quotient and the fist quotient 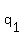 being multiples of being multiples of  , ,
 would be a multiple of would be a multiple of  . .
That means that the remainder from dividing  by by 
is the same as the remainder from dividing  by by  ,which is the final sum of digits for ,which is the final sum of digits for  , ,  : :

WHY THE PROBLEM AS POSTED DI NOT MAKE SENSE:
"When 64329 is divided by the number x" means 64329 ÷ x .
That number  is the divisor. is the divisor.
The phrase "successive remainders" suggests that
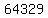 is divided by is divided by  to get a quotient and a remainder, to get a quotient and a remainder,
then that quotient is divided by  to get a second quotient and a second remainder, to get a second quotient and a second remainder,
and that second quotient is divided by  to get a third quotient and a third remainder. to get a third quotient and a third remainder.
That cannot happen with the remainders listed.
If in a first division, we divide 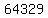 by by  , ,
getting quotient 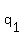 and remainder and remainder  , ,
we know that
 . .
So,  . .
As 32077 is a prime number, that would mean  . .
The phrase "successive remainders" suggests that
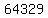 is divided by is divided by  to get a quotient to get a quotient 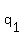 and and  as a remainder; as a remainder;
the quotient 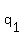 obtained in the first division is divided by obtained in the first division is divided by  again to get a second quotient again to get a second quotient 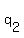 and and 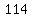 as a remainder, as a remainder,
and that second quotient 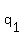 is divided by is divided by  getting a third quotient getting a third quotient 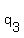 and and  as a remainder. as a remainder.
In the second division,  would be divided by would be divided by 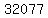 , ,
getting  as the quotient and as the quotient and  as a remainder. as a remainder.
Clearly, if dividing 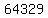 by by  gives gives  for a remainder, for a remainder,  would be would be 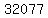 , the quotient would be , the quotient would be  , ,
and we would not get 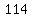 as a reminder when dividing as a reminder when dividing  by by  . .
If a number  that is not that is not 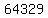
is divided by a divisor  (that may noy be the (that may noy be the  the problem is about) the problem is about)
to get a quotient 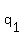 and and  as a remainder; as a remainder;
the quotient 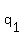 obtained in the first division is divided by obtained in the first division is divided by  again to get a second quotient again to get a second quotient 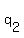 and and 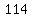 as a remainder, as a remainder,
and that second quotient 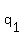 is divided by is divided by  getting a third quotient getting a third quotient 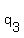 and and 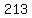 as a remainder, as a remainder,
 , ,  , and , and 
Then,
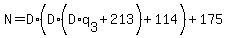
 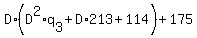
 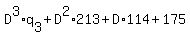
As the divisor must be greater than all remainders,
it must be a whole number that satisfies  . .
That makes for a pretty big number  to be divided. to be divided.
The smallest such number would be 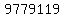 , ,
what we get with  and and  . .
|
|
|