|
Question 1100188: Triangle ABC is congruent to triangle DEF. Find the lengths of the given sides.
BC= x+17
EF= 4x+5
So BC= ?
and, EF= ?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! ABC is congruent with DEF means
AB=DE , BC=EF , AC=DF , angle ABC=angle DEF, etc.
As BC=EF ,  is the equation they want you to write and solve. is the equation they want you to write and solve.
That is algebra coming to haunt students who thought it was safe to forget algebra while taking geometry.
We solve equations by transforming them into easier ones.
and we can always do that by adding the same expression to both sides of the equal sign,
or by multiplying both sides of the equal sign times a nonzero real number:

After adding 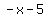 to both sides, we have to both sides, we have  , and we can multiply both sides of the equal sign times , and we can multiply both sides of the equal sign times  . .
(We are allowed to call that dividing by 3, but see it as a multiplication)
We get  , which simplifies to , which simplifies to  . .
The teacher wants you to plug  in place of in place of  in one of the expressions for the corresponding sides BC and EF. in one of the expressions for the corresponding sides BC and EF.
Or maybe the teacher wants yo to do that with both expressions and "show your work."
The expression for BC was  , so , so  , which simplifies to , which simplifies to  . .
I am confident that I did not make any mistake solving the equation,
and that EF=21 too, but maybe the teacher wants to see a verification.
The expression for EF was  , so , so  , which simplifies to , which simplifies to  and to and to  . .
That proves that the length found for sides BC and EF
(corresponding sides that should be congruent by CPCTC)
are the same,strongly suggesting that the equation was set up correctly,
and solved correctly.
Wordy explanation:
When we say two triangles are congruent,
we mean that they "are twins", that can be superimpose exactly,
and we say the vertices' letters in such an order
that the corresponding vertices are in the same place in the 3-letter sequence.
That means that when we move and/or flip DEF,
we can make A coincide with D,
at the same time as B coincides with E,
and C coincides with F.
That tells us that the distance BC (from B to C) is the same as EF (from E to F).
In geometry, we often invoke the fact that Corresponding Parts of Congruent Triangles are Congruent
(abbreviated CPCTC).
|
|
|
| |