Question 1100168: 3x^2-4y^2=32
2x^2+5y^2=52
and
x^2+y^2=64
x^2/64+y^2/9=1
Answer by ikleyn(52834)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
3x^2 - 4y^2 = 32 (1)
2x^2 + 5y^2 = 52 (2)
I will use the ELIMINATION method.
Multiply eq(1) by 2 (both sides). Multiply eq(2) by 3 (both sides).
You will get an equivalent system
6x^2 - 8y^2 = 64 (3)
6x^2 + 15y^2 = 156 (4)
Now coefficients at x^ are the same in both equations.
It was my goal to make them equal, and I reached this goal by multiplying equations.
Next step is to subtract eq(3) from eq(4). The terms with x^2 will cancel each other, and you get an equation for SINGLE unknown y:
15y^2 - (-8y^2) = 156 - 64, or
23y^2 = 92 ====> y^2 =  = 4 ====> y = +/- = 4 ====> y = +/- = +/-2.
Case 1. y = 2. ====> from eq(2) 2x^2 = 52 - 5y^2 = 52 - 5*4 = 32 ====> x^2 = = +/-2.
Case 1. y = 2. ====> from eq(2) 2x^2 = 52 - 5y^2 = 52 - 5*4 = 32 ====> x^2 = 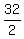 = 16 ====> x = +/- = 16 ====> x = +/-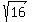 = +/-4.
Case 2. y = -2. ====> from eq(2) 2x^2 = 52 - 5y^2 = 52 - 5*4 = 32 ====> x^2 = = +/-4.
Case 2. y = -2. ====> from eq(2) 2x^2 = 52 - 5y^2 = 52 - 5*4 = 32 ====> x^2 = 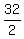 = 16 ====> x = +/- = 16 ====> x = +/-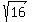 = +/-4.
Answer. There are 4 solutions. They are these pairs: (4,2), (4,-2), (-4,2) and (-4,-2).
Geometric interpretation: two ellipses centered at the coordinate origin, intersect in 4 points. = +/-4.
Answer. There are 4 solutions. They are these pairs: (4,2), (4,-2), (-4,2) and (-4,-2).
Geometric interpretation: two ellipses centered at the coordinate origin, intersect in 4 points.
-----------------
To see more similar solved problems of this type, look into the lesson
- Solving systems of algebraic equations of degree 2
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Systems of equations that are not linear".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
======================
Please do not post more than one problem to each post.
It is THE RULE of this forum.
When you violate this rule, you work AGAINST your better interests.
|
|
|