SOLUTION: Mary Jo spends $2,860 to buy stock in two companies. She pays $13 a share to one of the companies and $26 a share to the other. If she ends up with a total of 150 shares, how many

Let x be the number of shares at $13 and

let y be the number of shares at $26.


Then you have these two equations

  x +   y =  150,             (1)     (counting shares)
13x + 26y = 2860  dollars     (2)     (counting dollars)


These are your basic equations, and as soon as you got this system, the setup is completed.


There are different methods of solving such system (Substitution, Elimination, using determinants). 

I will use the Elimination method here. 
Divide equation (2) by 13 (both sides, You will get this equation in this equivalent form

x + 2y = 220.             (3)


Now subtract eq(3) from eq(1).  x-terms will cancel each other, and  you will get an expression for unknown y

y =  220-150 = 70.      


Thus, you found number of shares at $26. It is 70. 


Hence the number of shares at $13 was 150 - 70 = 80.


Check.  80*13 + 26*70 = 2860 dollars.   ! Correct. !


Answer.  80 shares at $13 and 70 shares at $26.

Let x be the number of shares at $13.

Then the number of shares at $6 is (15-x),  according to the condition.


It was payed  13*x        dollars for x        13-dollar shares.

It was payed  26*(150-x)  dollars for (150-x)  26-dollar shares.

Summing up these money, you get the "money" equation

13x + 26*(150-x) = 2860.     (4)


It is your basic equation in the frame of this approach,
and as soon as you got this equation, the setup is completed.


To solve equation (4), simplify it step by step.

13x + 3900 - 26x = 2860  ====>  -13x = 2860 - 3900 = -1040  ====>  x = 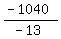 = 80.


Thus you get 80 shares at $13 dollars.


Surely, you got the same answer.

Let assume for a minute that all shares are at $13.

Then their total cost would be 150*13 = 1950 dollars.

But it is by 2860 - 1950 = 910 dollars less than the given total cost.


Why did we get the difference ?  - But of course, because we account 26-dollar shares as 13-dollar shares.

So, we should return these 26-dollar shares back. Returning each, we diminish the difference of $910 by  26-13 = 13 dollars.

Then it is clear that the number of 26-dollar shares was   = 70,  exactly as in the solutions 1 and 2 above.


Hence, the number of $13 shares was  150 - 70 = 80, 
and you got the same answer.