SOLUTION: Find the exact value of the expression or state that it does not exist: csc^-1 (-2) a.The value of csc^-1 x is an angle in what interval? b. Let csc^-1(-2) = θ such th

Algebra ->  Trigonometry-basics -> SOLUTION: Find the exact value of the expression or state that it does not exist: csc^-1 (-2) a.The value of csc^-1 x is an angle in what interval? b. Let csc^-1(-2) = θ such th      Log On


   

Question 1099758: Find the exact value of the expression or state that it does not exist:
csc^-1 (-2)
a.The value of csc^-1 x is an angle in what interval?
b. Let csc^-1(-2) = θ such that sin^-1 = ___ and sinθ= ____
c. Is the value of sinθ positive, negative, or equal to 0?
d. does the angle θ: lie in the interval 0<θ<π/2 , is equal to π/2, or lies in the interval -π/2<θ<0
e. Where does the terminal side of angle θ lie?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
y=csc%5E%28-1%29%28x%29 (alternatively represented as y=arccsc%28x%29
is the inverse function of y=csc%28x%29=1%2Fsin%28x%29 .
The graph of y=csc%28x%29=1%2Fsin%28x%29 looks like this:

.
The function y=csc%28x%29=1%2Fsin%28x%29 is a periodic function,
like all trigonometric functions,
so the inverse can only be defined by restricting the domains for the x values, so as not to repeat y values.
That would be taking only the part of the graph between the blue lines,
to get a function defined as
y=csc%28x%29=1%2Fsin%28x%29 for -pi%2F2%3C=x%3C=pi%2F2 only
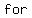
(quadrants I and IV).

Then we, can interchange the variables and define
y=csc%5E%28-1%29%28x%29 is the angle y ,
between -pi%2F2 and pi%2F2
such that csc%28y%29=x
That is the same approach used to define the inverse of y=sin%28x%29 .

So,
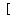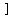a. The value of the function y=csc%5E%28-1%29%28x%29 is an angle theta in the interval %22%5B%22-pi%2F2%22%2C%22pi%2F2%22%5D%22 or highlight%28-pi%2F2%3C=x%3C=pi%2F2%29.

b. What is sin^-1 supposed to mean? 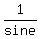1%2Fsine ?
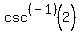csc%5E%28-1%29%282%29 is the angle theta , with -pi%2F2%3C=x%3C=pi%2F2 that has
csc%28theta%29=1%2Fsin%28theta%29=%28sin%28theta%29%29%5E%28-1%29=highlight%28-2%29
and sin%28theta%29=highlight%28-1%2F2%29 .

NOTE:
We know that in quadrant I sin%28pi%2F6%29=1%2F2 (or sin%2830%5Eo%29=1%2F2 .
In quadrant IV, using the symmetrical quadrant I angle as reference,
we find that sin%28-pi%2F6%29=-1%2F2 ,
so csc%5E%28-1%29%282%29=-pi%2F6 .
However, this question wants you to crawl to the answer very, very slowly.

c. Is the value of sinθ positive, negative, or equal to 0?
In part b. we found that we are looking for an angle whose sine is -1%2F2 , so we know that -1%2F2 is highlight%28negative%29 .

d. An angle theta that has a negative sine,
and is in the interval we agreed to in part b.
has to be in the interval 0%3Ctheta%3C=pi%2F2

e. The terminal side of angle theta lies in quadrant IV.
Here it is:
It is a negative angle because it is a counterclockwise turn from the positive x-axis.