SOLUTION: Find the equation of the line tangent to the circle x2 + y2 = 25 at point (3,4)

Click here to see ALL problems on test

Question 1099730: Find the equation of the line tangent to the circle x2 + y2 = 25 at point (3,4)
Found 5 solutions by Fombitz, htmentor, Boreal, ikleyn, MathTherapy:
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website!

The slope of the tangent line is equal to the value of the derivative at the tangent point,

So using point-slope form,

.
.
.
.

Answer by htmentor(1343)   (Show Source):
You can put this solution on YOUR website!
Using implicit differentiation we have 2xdx + 2ydy = 0 -> dy/dx = -x/y
So the slope of the tangent line is -x/y = -3/4

Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website!
y^2=25-x^2
2ydy/dx=-2x
dy/dx=-x/y
when x=3, y'=-3/4
use point slope formula y-y1=m(x-x1), m slope and (x1, y1) point.
y-4=(-3/4)(x-3)
y=(-3/4)x+6.25

Answer by ikleyn(52786)   (Show Source):
You can put this solution on YOUR website!
.
YOU DO NOT NEED CALCULUS to answer this question.

Elementary algebra PLUS Elementary geometry is fully enough !.
-----------------

The vector from the center (which is the coordinate origin) to the tangent point is (x,y) = (3,4). Its slope is . The tangent line is perpendicular to the radius drawn to the tangent point. Hence, the tangent line has the slope . Then the equation of the tangent line is y - 4 = , or, after multiplying both sides by 4, 4y - 16 = (-3)*(x-3), or, equivalently, 3x + 4y = 25. What's it.

Solved.

---------------------------------------------------
A S     S I M P L E     A S     P O S S I B LE
---------------------------------------------------

Answer by MathTherapy(10552)   (Show Source):
You can put this solution on YOUR website!

Find the equation of the line tangent to the circle x2 + y2 = 25 at point (3,4)

Calculus is UNNECESSARY here. How many people who ask questions on here know calculus? Help these people with the SIMPLEST steps so they can understand.
Looking at the the equation of the circle, the center is located at the origin, or at coordinate point: (0, 0). With the point of tangency being (3, 4), the slope of the radius line is:
Now, as a tangent and radius line intersect at a perpendicular point, it follows that the tangent line's slope is .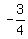
With the tangent line's point of (3, 4), and a slope of 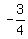, we use the point-slope form, or to find the equation of the tangent line