Question 1099697: ABC electric uses this formula, f(x)=750 -10x, to depreciate computers, where f is the value of a computer and x is the number of months since itís purchase.
What is the meaning of f(36)?
What is the meaning of b in f(b)? What is the value of b ?
Write a formula for f^-1, and explain what it means in this situation.
When will the depreciated value of a computer be less than $400 ?
What is the meaning of c in f^-1(c)= 60 ? What is the value of c ?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your equation is f(x) = 750 - 10x.
f(x) represents the value of the car after it has been depreciated for x months.
f(36) represents the value of the car after it has been depreciated for 36 months.
the value of the car depreciates 10 dollars in value for every month that it is in service.
f(b) tells you the value of the car after it has been in service for b months.
the formula becomes f(b) = 750 - 10 * b.
the value of b is not known.
you either have to assign a value to b, or you have to assign a value for f(b) and then solve for b.
f^-1(x) is the inverse function of f(x).
you find the inverse function as follows:
let y = f(x).
formula becomes y = 750 - 10x
solve for x to get x = (750 - y) / 10
replace y with x and x with y and you get y = (750 - x) / 10
replace y with f^-1(x) and you get f^-1(x) = (750 - x) / 10
in the inverse function, x represents the value of the car and y represents the number of months the car has been in service.
the normal function solves for the value of the car after it has been in service for x months and the inverse function solves for the number of months the car has been in service when it's value is equal to x.
the inverse function essentially reverses the normal function.
when you solved for f(36) in the normal function, your solution was f(36) = 390, so the coordinate point of the solution is (36,390).
when you solved for f(390) in the inverse function, your solution was f(390) = 36, so the coordinate point of the solution is (390,36).
this is what they mean when they say that (x,y) in the normal function is equal to (y,x) in the inverse function.
if you graph the inverse function, it will be a reflection of the normal funciton about the line y = x.
the graph looks like this.
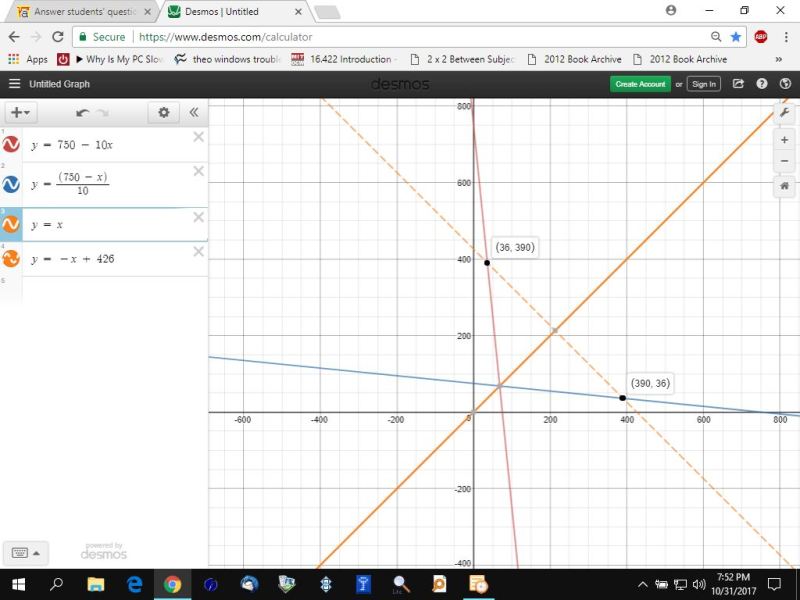
in this graph, the red line is the graph of the normal function and the blue line is the graph of the inverse function.
the solid orange line is the graph of y = x.
the dashed orange line is the graph of y = -x + 426.
this line is perpendicular to the line y = x, so it serves as a distance measure between the normal function and the inverse function and the line y = x.
since the two points are reflections about the line y = x, their distance from the line y = x is the same.
the dashed line is only there to provide intersection points so you can see that the point (36,390) is a reflection of the point (390,36) about the line y = x.
if you want to know when the depreciated value of the car will be less than 400, you can use the inverse function to find that value.
the inverse function is y = (750 - x) / 10
x is the value of the car and y is the number of months in service.
when x is 400, the inverse function becomes y = (750 - 400) / 10.
this becomes y = 350 / 10 which results in y = 35.
the number of months is 35 when the value of the car is 400.
you already know that the value of the car is 390 when x = 36, therefore, you can deduce that the value of the car will be less than 400 when x is greater than 35.
your last question is what is the value of c in f^-1(c) = 60
the inverse function is f^-1(x) = (750 - x) / 10
f^-1(c) = (750 - c) / 10
you just replace x with c.
when f^-1(c) = 60, f^-1(c) = (750 - c) / 10 becomes 60 = (750 - c) / 10.
now you want to solve for c.
multiply both sides of this equation by 10 to get 600 = 750 - c
add c to both sides of this equation and subtract 600 from both sides of this equation to get c = 750 - 600 which results in c = 150.
what this is telling you is that the value of the car is 150 when the number of months in service is 60.
you can use the normal function to confirm this.
the normal function is f(x) = 750 - 10x
x is the number of months in service which is 60.
the function becomes f(x) = 750 - 10 * 60 which becomes f(x) = 750 - 600 which results in f(x) = 150.
the normal function tells you that value of the car is 150 when the car is in service for 60 months.
the inverse function tells you that the number of months that the car is in service is 60 when the value of the car is 150.
here's a reference that might help you understand the concept a little better.
https://www.mathsisfun.com/sets/function-inverse.html
|
|
|