Question 1099658: By eating 1 egg, 1 cupcake, and 1 slice of pizza, a child consumes 301 mg of cholesterol. If
the child eats 3 cupcakes and 4 slices of pizza, he or she takes in 92 mg of cholesterol. By eating 2 eggs and 1 cupcake, a child consumes 566 mg of cholesterol. How much cholesterol is in each item?
Found 2 solutions by richwmiller, ikleyn:
Answer by richwmiller(17219)   (Show Source): (Show Source):
You can put this solution on YOUR website! By eating 1 egg, 1 cupcake, and 1 slice of pizza, a child consumes 301 mg of cholesterol.
1e+1c+1s=301
If the child eats 3 cupcakes and 4 slices of pizza, he or she takes in 92 mg of cholesterol.
0e+3c+4s=92
By eating 2 eggs and 1 cupcake, a child consumes 566 mg of cholesterol. How much cholesterol is in each item?
2e+1c+0s=566
0e+3c+4s=92
1e+1c+1s=301
Answer by ikleyn(52886)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
From the condition, you get this system of 3 equations in 3 unknowns
1e + 1c + 1s = 301, (1)
3c + 4s = 92, (2)
2e + 1c = 566. (3)
Let solve it step by step. I will use the Elimination method.
First step ADD eq(3) to eq(2) (both sides). After adding, you will get
2e + 4c + 4s = 658. (4) (658 = 566 + 92)
Next step multiply eq(1) by 4 (both sides). You will get
4e + 4c + 4s = 1204. (5)
Now notice that the terms 4c + 4s are the same in (4) and (5),
It was my goal to do it, when I made my transformations.
Next step SUBTRACT eq(4) from eq(5) (both sides). The terms 4c + 4s will cancel each other, and as a result, you will get
2e = 1204 - 658 = 546.
It gives you e =  = 273.
Thus you just found the value of e. It is 273, or 273 mg of cholesterol in one egg.
OK, very good. Now substitute this value of e into eq(3). You will get
2*273 + 1c = 566, or c = 566 - 2*273 = 20.
Thus you found the value of c. It is 20, or 20 mg of cholesterol in one cupcake.
The last step is to find s. For it, substitute the found value of "c" into eq(2).
You will get
3*20 + 4s = 92 ====> 4s = 92 - 3*20 = 32 ====> s = = 273.
Thus you just found the value of e. It is 273, or 273 mg of cholesterol in one egg.
OK, very good. Now substitute this value of e into eq(3). You will get
2*273 + 1c = 566, or c = 566 - 2*273 = 20.
Thus you found the value of c. It is 20, or 20 mg of cholesterol in one cupcake.
The last step is to find s. For it, substitute the found value of "c" into eq(2).
You will get
3*20 + 4s = 92 ====> 4s = 92 - 3*20 = 32 ====> s = 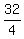 = 8.
The problem is solved, and you ONLY NEED to check the solution. For it, substitute the found value
into each of the original equations and calculate the left side; then compare with the right side.
eq(1): 1e + 1c + 1s = 273 + 20 + 8 = 301. ! Correct !
eq(2): 3c + 4s = 3*20 + 4*8 = 92. ! Correct !
eq(3): 2e + 1c = 2*273 + 20 = 566. ! Correct !
Answer. 273 mg of cholesterol in 1 egg; 20 mg of cholesterol in 1 cupcake, and 8 mg of cholesterol in 1 slice of pizza. = 8.
The problem is solved, and you ONLY NEED to check the solution. For it, substitute the found value
into each of the original equations and calculate the left side; then compare with the right side.
eq(1): 1e + 1c + 1s = 273 + 20 + 8 = 301. ! Correct !
eq(2): 3c + 4s = 3*20 + 4*8 = 92. ! Correct !
eq(3): 2e + 1c = 2*273 + 20 = 566. ! Correct !
Answer. 273 mg of cholesterol in 1 egg; 20 mg of cholesterol in 1 cupcake, and 8 mg of cholesterol in 1 slice of pizza.
We solved the problem, and on the way you learned a bit on how the Elimination method works.
To learn more about it, see my lessons
- Solving systems of linear equations in 3 unknowns by the Substitution method,
- BRIEFLY on solving systems of linear equations in 3 unknowns by the Substitution method,
- Solving systems of linear equations in 3 unknowns by the Elimination method and
- BRIEFLY on solving systems of linear equations in 3 unknowns by the Elimination method
- OVERVIEW of LESSONS on solving systems of linear equations in three unknowns by the Substitution and/or Elimination methods
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic
"3x3-Matrices, determinants, Cramer's rule for systems in three unknowns"
In addition, there are many free of charge SOLVERS on a Cramer's rule in the internet.
One of such popular solvers is in this site under the link
https://www.algebra.com/algebra/homework/Matrices-and-determiminant/cramers-rule-3x3.solver
https://www.algebra.com/algebra/homework/Matrices-and-determiminant/cramers-rule-3x3.solver
|
|
|